题目内容
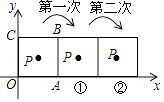
【题目】如图,半圆O的半径OA=4,P是OA延长线上一点,线段OP的垂直平分线分别交OP、半圆O于B、C两点,射线PC交半圆O于点D.设PA=x,CD=y,则能表示y与x的函数关系的图象是( )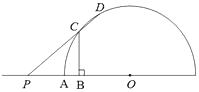
A.
B.
C.
D.
【答案】A
【解析】解:设AO与半圆O的另一个交点为点E,
如图1,由题意可知,线段OP的垂直平分线交半圆O于点C,且PC与半圆O相切时,点C与点D重合,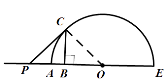
图1
此时,∵PC与半圆O相切,PC![]() OC,且BC是OP的垂直平分线,
OC,且BC是OP的垂直平分线,
∴△ PCO是等腰直角三角形,∴PO=![]() ,
,
∴PA=![]() -4,
-4,
分 0<x<![]() -4 和
-4 和 ![]() -4<x<4 以下两种情况:
-4<x<4 以下两种情况:
①当0<x<![]() -4时,如图2:
-4时,如图2: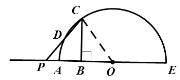
图2
∵OA=4,PA=x,CD=y,
∴根据切割线定理的推论及垂直平分线性质(PC=OC)得:PA![]() PE=PD
PE=PD![]() PC,即x(x+8)=(4-y)
PC,即x(x+8)=(4-y)![]() 4,解得:y=
4,解得:y=![]() x2-2x+4(0<x<
x2-2x+4(0<x<![]() -4).
-4).
②当![]() -4<x<4时,如图3:
-4<x<4时,如图3: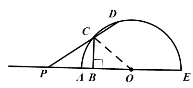
图3
∵OA=4,PA=x,CD=y,
∴根据切割线定理的推论及垂直平分线性质(PC=OC)得:PA![]() PE=PC
PE=PC![]() PD,即x(x+8)=4(4+y),解得:y=
PD,即x(x+8)=4(4+y),解得:y=![]() x2+2x-4(
x2+2x-4(![]() -4<x<4).
-4<x<4).
③当x![]() 4时,显然不成立.
4时,显然不成立.
综上,可知对应函数图像应为选项A.
【考点精析】本题主要考查了二次函数的图象的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】如图,在一次测量活动中,小丽站在离树底部E处5m的B处仰望树顶C,仰角为30°,已知小丽的眼睛离地面的距离AB为1.65m,那么这棵树大约有多高?(结果精确到0.1m,参考数据: ![]() ≈1.73)
≈1.73)
【题目】如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则 ①DE=DF;②DF=EF;③△DCF≌△DGE;④EF= ![]() .
.
上面结论正确的有( )
A.1个
B.2个
C.3个
D.4个
【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7
乙:5,7,8,7,8,9,7,9,10,10
丙:7,6,8,5,4,7,6,3,9,5
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | |
乙 | 8 | 8 | 2.2 |
丙 | 6 | 3 |
(2)根据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定,求甲、乙相邻出场的概率.