题目内容
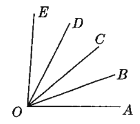
【题目】如图,已知∠AOB=20°,∠AOE=86°,OB平分∠AOC,OD平分∠COE.
(1)∠COD的度数是______;
(2)若以O为观察中心,OA为正东方向,射线OD在什么位置?
(3)若以OA为钟面上的时针,OD为分针,且OA正好在“时刻3”的下方不远,求出此时的时刻.(结果精确到分钟)
【答案】(1)23°;(2)北偏东27°;(3)此时的时刻为3时![]() 分.
分.
【解析】
(1)根据角平分线的性质,可得∠AOC的度数,根据角的和差,可得∠COE,根据角平分线的性质,可得答案;
(2)根据角的和差,可得∠AOD的度数,根据方向角的表示方法,可得答案;
(3)设3时x分,时针与分针相距63°,由(90°+时针旋转的角度)减去分针旋转的角度,列方程求解即可.
(1) 由OB平分∠AOC,∠1=20°,得∠AOC=40°,
由角的和差,得∠COE=∠AOE-∠AOC=86°-40°=46°,
由OD平分∠COE,得∠COD=![]() ∠COE=
∠COE=![]() ×46°=23°;
×46°=23°;
(2)∠AOD=∠AOE-∠EOD=86°-23°=63°,
∴射线OD在东偏北63°,即在北偏东27°;
(3)设3时x分,时针与分针相距63°,由(90°+时针旋转的角度)减去分针旋转的角度,得
![]() .
.
∴此时的时刻为3时![]() 分
分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目