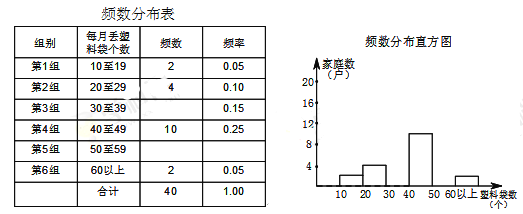
��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�������y��![]() x2������A��x1��y1����C��x2��y2��������x1��x2�Ƿ���x2��2x��8��0����������x1��x2������A��ֱ��l��������ֻ��һ��������
x2������A��x1��y1����C��x2��y2��������x1��x2�Ƿ���x2��2x��8��0����������x1��x2������A��ֱ��l��������ֻ��һ��������
��1����A��C��������ꣻ
��2����ֱ��l�Ľ���ʽ��
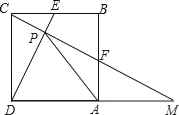
��3����ͼ2����B���߶�AC�ϵĶ��㣬������B��y���ƽ����BE��ֱ��l�ཻ�ڵ�E�����������ཻ�ڵ�D������E��DC��ƽ����EF��ֱ��AC�ཻ�ڵ�F����BF�ij���
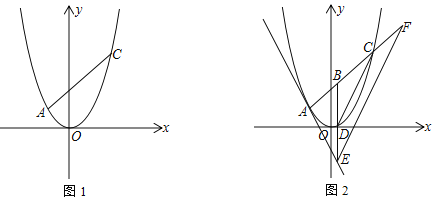
���𰸡���1��A����2��2����C��4��8�� ��2��y����2x��2 ��3��![]()
��������
��1����һԪ���η��̼��ɵó���A��C���ꣻ
��2�������ֱ��l�Ľ���ʽ�������������߽���ʽ��������0�����k��ֵ�����ɵó�ֱ��l�Ľ���ʽ��
��3�������B�����꣬�������BC���ٱ�ʾ����D��E�����꣬�����ó�BD��BE�����жϳ���BDC�ס�BEF�ó�����ʽ�������̼������BF��
��1����x1��x2�Ƿ���x2��2x��8��0����������x1��x2��
��x1����2��x2��4��
��A����2��2����C��4��8����
��2������ֱ��l�Ľ���ʽΪy��kx+b��k��0����
��A����2��2����ֱ��l�ϣ�
��2����2k+b��
��b��2k+2��
��ֱ��l�Ľ���ʽΪy��kx+2k+2�٣�
��������y��![]() x2�ڣ�
x2�ڣ�
�����٢ڻ���ã�x2��2kx��4k��4��0��
��ֱ��l��������ֻ��һ�������㣬
�������2k��2��4����4k��4����4k2+16k+16��4��k2+4k+4����4��k+2��2��0��
��k����2��
��b��2k+2����2��
��ֱ��l�Ľ���ʽΪy����2x��2��
��ƽ����y���ֱ�ߺ�������y��![]() x2ֻ��һ�����㣬
x2ֻ��һ�����㣬
��ֱ��l����A����2��2����
��ֱ��l��x����2��
��3���ɣ�1��֪��A����2��2����C��4��8����
��ֱ��AC�Ľ���ʽΪy��x+4��
���B��m��m+4����
�ߣ�4.8����
��BC��![]() |m��4|��
|m��4|��![]() ��4��m��
��4��m��
�߹���B��y���ƽ����BE��ֱ��l�ཻ�ڵ�E�����������ཻ�ڵ�D��
��D��m��![]() m2����E��m����2m��2����
m2����E��m����2m��2����
��BD��m+4��![]() m2��BE��m+4������2m��2����3m+6��
m2��BE��m+4������2m��2����3m+6��
��DC��EF��
���BDC�ס�BEF��
��![]() ��
��
��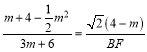 ��
��
��BF��6![]() ��
��