题目内容
【题目】阅读理解:
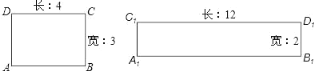
给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的 2 倍,则这个矩形是给定矩形的“加倍”矩形.如图,矩形 A1B1C1D1是矩形 ABCD 的“加倍”矩形.请你解决下列问题:
(1)边长为 a 的正方形存在“加倍”正方形吗?如果存在,求出“加倍”正方形的边长;如果不存在,说明理由.
(2)当矩形的长和宽分别为 m,n 时,它是否存在“加倍”矩形?请作出判断,说明理由.
【答案】(1)不存在.理由见解析;(2)存在.理由见解析.
【解析】
(1)根据所有的正方形都相似由相似比确定面积比后即可做出判断;
(2)设“加倍”矩形的长和宽分别为x,y,可得![]() 的关系,分析可得x,y就是关于A的方程A2-2(m+n)A+2mn=0的两个正根,判断可得:△=4(m2+n2)>0,故存在“加倍”矩形.
的关系,分析可得x,y就是关于A的方程A2-2(m+n)A+2mn=0的两个正根,判断可得:△=4(m2+n2)>0,故存在“加倍”矩形.
根据给出的两边长得到周长,然后设出其中一边,表示出另一边根据题意列出方程求解,若能求得答案即存在,否则就不存在.
(1)不存在.
因为两个正方形是相似图形,当它们的周长比为 2 时,则面积比必定是 4,所以不存在.
(相同解答均可给分,如:满足周长是 2 倍时,则面积就成了 4 倍,所以不存在)
(2)存在.
设“加倍”矩形的长和宽分别为 x,y.
则:![]() .
.
x,y 就是关于 A 的方程 A2﹣2(m+n)A+2mn=0 的两个正根.
∵△=[﹣2(m+n)]2﹣8mn=4(m2+n2).
此题中,m>0,n>0.
∴△=4(m2+n2)>0.
∴方程有两个不相等的正实数根 x 和 y.
即:存在一个矩形是已知矩形的“加倍”矩形.

练习册系列答案
相关题目