题目内容
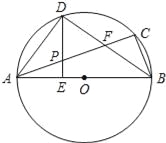
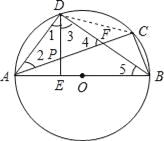
【题目】已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.
【答案】(1)证明见试题解析;(2)证明见试题解析;(3)2.5,2.4.
【解析】试题(1)利用角平分线的性质得出∠CBD=∠DBA,进而得出∠DAC=∠DBA;
(2)利用圆周角定理得出∠ADB=90°,进而求出∠PDF=∠PFD,则PD=PF,求出PA=PF,即可得出答案;
(3)利用勾股定理得出AB的长,再利用三角形面积求出DE即可.
试题解析:(1)∵BD平分∠CBA,∴∠CBD=∠DBA,∵∠DAC与∠CBD都是弧CD所对的圆周角,
∴∠DAC=∠CBD,∴∠DAC=∠DBA;
(2)∵AB为直径,
∴∠ADB=90°,
∵DE⊥AB于E,
∴∠DEB=90°,
∴∠1+∠3=∠5+∠3=90°,
∴∠1=∠5=∠2,
∴PD=PA,
∵∠4+∠2=∠1+∠3=90°,且∠ADB=90°,
∴∠3=∠4,
∴PD=PF,
∴PA=PF,即P是线段AF的中点;
(3)连接CD,
∵∠CBD=∠DBA,
∴CD=AD,
∵CD﹦3,∴AD=3,
∵∠ADB=90°,
∴AB=5,
故⊙O的半径为2.5,
∵DE×AB=AD×BD,
∴5DE=3×4,
∴DE=2.4.
即DE的长为2.4.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案【题目】如图所示的港珠澳大桥是目前桥梁设计中广泛采用的斜拉桥,它用粗大的钢索将桥面拉住,为检测钢索的抗拉强度,桥梁建设方从甲、乙两家生产钢索的厂方各随机选取5根钢索进行抗拉强度的检测,数据统计如下(单位:百吨)

甲、乙两厂钢索抗拉强度检测统计表
钢索 | 1 | 2 | 3 | 4 | 5 | 平均数 | 中位数 | 方差 |
甲厂 | 10 | 11 | 9 | 10 | 12 | 10.4 | 10 | 1.04 |
乙厂 | 10 | 8 | 12 | 7 | 13 | a | b | c |
(1)求乙厂5根钢索抗拉强度的平均数a(百吨)、中位数b(百吨)和方差c(平方百吨).
(2)桥梁建设方决定从抗拉强度的总体水平和稳定性来决定钢索的质量,问哪一家的钢索质量更优?