题目内容
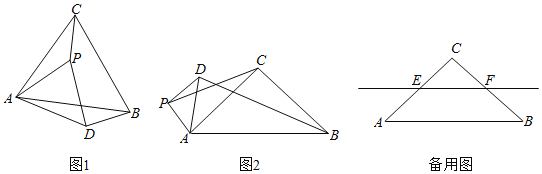
【题目】如图,在![]() 中,
中,![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,点
,点![]() 关于线段
关于线段![]() 的对称点为点
的对称点为点![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点,连接
上的一个动点,连接![]() 、
、![]() 、
、![]() 、
、![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,
,![]() ,当
,当![]() 的值最小时,则
的值最小时,则![]() 的值为( )
的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
设点M和点B关于AC对称,F为EM与AC交点,过点E作EG⊥AC于G,过点E作EN⊥BC,交BC延长线于点N,根据题意得出当EF+BF最小时点F的位置,再通过平行线的性质得到∠EAG=∠BDC,从而求出EG的长,再判定四边形EGCN为矩形,得到CN,最后利用△MFC∽MEN将![]() 转化为
转化为![]() 求值即可.
求值即可.
解:当EF+BF最小时,如图,点M和点B关于AC对称,F为EM与AC交点,过点E作EG⊥AC于G,过点E作EN⊥BC,交BC延长线于点N,
此时EF+BF的最小值即为EF+FM,即EM,
∵AC=![]() ,点D为AC中点,BC=2,
,点D为AC中点,BC=2,
∴AD=CD=![]() ,
,
∴tan∠BDC=![]() ,
,
∵AE∥BD,
∴∠EAG=∠BDC,
∴tan∠EAG=![]() =
=![]() ,设EG=x,
,设EG=x,
∴AG=![]() x,而AE=
x,而AE=![]() ,
,
在△AEG中, ,
,
解之得:x=![]() 或
或![]() (舍),
(舍),
由题意可得:∠N=∠ACB=∠EGC=90°,
∴四边形EGCN为矩形,
∴EG=NC=![]() ,
,
∵AC⊥BC,EN⊥BC,
∴AC∥EN,
∴△MFC∽MEN,
∴![]() ,则
,则![]() ,
,
故选C.


练习册系列答案
相关题目