题目内容
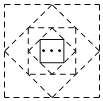
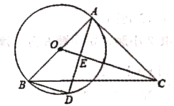
【题目】如图,正方形![]() 中,
中,![]() 为
为![]() 边上任意点,
边上任意点,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() .
.
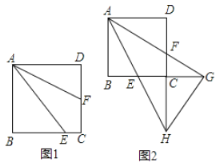
(1)如图1,当点![]() 恰好为
恰好为![]() 中点,延长
中点,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;
;
(2)在(1)的条件下,求证:![]() ;
;
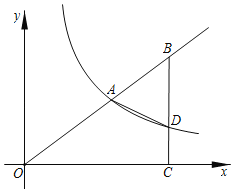
(3)如图2,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)由平行线的性质和等角对等边,即可得到结论成立;
(2)利用“AAS”证△ADF≌△GCF得AD=CG,据此知CG=BC=BE+CE,根据EG=BE+CE+CE=BE+2CE=AE即可得证;
(3)连接DG,证△ADF≌△DCG得∠CDG=∠DAF,再证△AFH∽△DFG得![]() ,结合∠AFD=∠HFG,知△ADF∽△HGF,从而得出∠ADF=∠FGH,根据∠ADF=90°即可得证.
,结合∠AFD=∠HFG,知△ADF∽△HGF,从而得出∠ADF=∠FGH,根据∠ADF=90°即可得证.
解:(1)∵AD∥CG,
∴∠DAF=∠G,
又∵AF平分∠DAE,
∴∠DAF=∠EAF,
∴∠G=∠EAF,
∴EA=EG,
(2)∵点F为CD的中点,
∴CF=DF,
又∵∠DFA=∠CFG,∠FAD=∠G,
∴△ADF≌△GCF(AAS),
∴AD=CG,
∴CG=BC=BE+CE,
∴EG=BE+CE+CE=BE=2CE=AE;
(3)如图所示,连接DG,
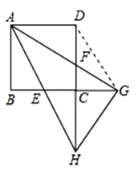
∵CG=DF,DC=DA,∠ADF=∠DCG,
∴△ADF≌△DCG(SAS),
∴∠CDG=∠DAF,
∴∠HAF=∠FDG,
又∵∠AFH=∠DFG,
∴△AFH∽△DFG,
∴![]() ,
,
又∵∠AFD=∠HFG,
∴△ADF∽△HGF,
∴∠ADF=∠FGH,
∵∠ADF=90°,
∴∠FGH=90°,
∴AG⊥GH.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目