题目内容
【题目】如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．若AB=8，AD=6 
，AF=4 ，则AE的长为 ．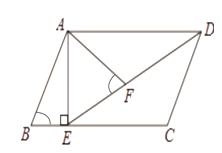 
【答案】6
【解析】因为AD∥BC CD=AB=8 所以∠ADF=∠DEC 因为∠AFE=∠B，∠B+∠C=∠AFE+∠AFD=180°
所以∠AFD=∠C，在△AFD和△DCE中， ∠ADF=∠DEC ∠AFD=∠C 所以△ADF∽△DEC
所以 
，即 
，解得：DE=12，根据Rt△ADE的勾股定理可得：AE=6．
【考点精析】解答此题的关键在于理解平行线的性质的相关知识，掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补，以及对平行四边形的性质的理解，了解平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
