题目内容
【题目】如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,BC上,EF与BD交于G,且∠DEF=60°,若AD=3,AE=2,则sin∠BEF= . 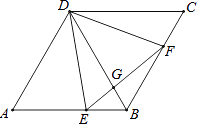
【答案】![]()
【解析】解:作EH⊥AD于H,如图所示:
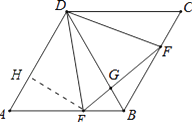
则∠AEH=90°﹣∠A=60°,
∴AH= ![]() AE=1,
AE=1,
∴EH= ![]() =
= ![]() ,
,
∵AD=3,
∴DH=AD﹣AH=2,
在Rt△DEH中,根据勾股定理得,DE= ![]() =
= ![]() ,
,
∵∠DEF+∠BEF=∠A+∠ADE,∠DEF=60°=∠A,
∴∠BEF=∠ADE,
∴sin∠BEF=sin∠ADE= ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用三角形的外角和含30度角的直角三角形的相关知识可以得到问题的答案,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目