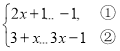题目内容
【题目】已知关于x的一元二次方程ax2＋bx＋c＝0的两实数根为x1，x2，根据一元二次方程解的意义和因式分解法解一元二次方程可知，x1，x2也是（x﹣x1）（x﹣x2）＝0的两个实数根，所以ax2＋bx＋c＝a（x﹣x1）（x﹣x2）．
利用这个结论可以解决一些相关问题．
（1）实数范围内因式分解：
例：分解因式2x2＋2x﹣1
解：令2x2＋2x﹣1＝0，解这个方程，得
＝
.
即x1＝
，x2＝
.
所以 2x2＋2x﹣1＝
．
试仿照上例在实数范围内分解因式：x2﹣6x＋1；
（2）解不等式：x2＋2x﹣1＞0；
（3）灵活运用：
已知方程（x﹣a）（x﹣b）﹣x＝0的两个实数根是c、d，求方程（2x﹣c）（2x﹣d）＋2x＝0的根．
【答案】（1）
；（2）
，或
；（3）x1＝
，x2＝
.
【解析】
（1） 根据题意设x2－6x＋1＝0，解得x的值再代入方程即可.
（2） 根据题意设x2＋2x－1＝0，解得x的值再代入不等式，解得不等式组即可.
（3） 将方程（x﹣a）（x﹣b）﹣x＝0的两根c、d代入方程，再把x=a代入方程即可解得方程的根.
解：（1）令x2－6x＋1＝0，解这个方程，得
.
所以，x2－6x＋1＝.
（2）令x2＋2x－1＝0，解这个方程，得
.
所以 x2＋2x－1＝
.
所以 ＞0.
所以 
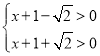，或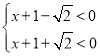
.
解这两个不等式组，得
，或.
（3）因为方程（x﹣a）（x﹣b）﹣x＝0的两根是c、d，
所以 （x﹣a）（x﹣b）﹣x＝（x－c）（x－d）.
所以 （x－c）（x－d）＋x＝（x﹣a）（x﹣b）.
因为当x＝a时，代入上式，得
（a－c）（a－d）＋a＝（a﹣a）（a﹣b）＝0，
所以x＝a是方程（x－c）（x－d）＋x＝0的一个根，
同理，x＝b也是方程（x－c）（x－d）＋x＝0的一个根.
所以方程 （x－c）（x－d）＋x＝0的两个根为x＝a或b.
在方程（2x﹣c）（/span>2x﹣d）＋2x＝0中，设2x＝y，得（y﹣c）（y﹣d）＋y＝0.
所以 y＝a或b.
所以 2x＝a或b，解得x1＝，x2＝.
所以，方程（2x﹣c）（2x﹣d）＋2x＝0的根是x1＝，x2＝.
