题目内容
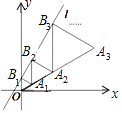
【题目】如图,在平面直角坐标系中,直线l:y=![]() 与y轴交于点B1,以OB1为一边在OB1右侧作等边三角形A1OB1,过点A1作A1B2平行于y轴,交直线l于点B2,以A1B2为一边在A1B2右侧作等边三角形A2A1B2,过点A2作A2B3平行于y轴,交直线l于点B3,以A2B3为一边在A2B3右侧作等边三角形A3A2B3,……则点A2019的纵坐标是( )
与y轴交于点B1,以OB1为一边在OB1右侧作等边三角形A1OB1,过点A1作A1B2平行于y轴,交直线l于点B2,以A1B2为一边在A1B2右侧作等边三角形A2A1B2,过点A2作A2B3平行于y轴,交直线l于点B3,以A2B3为一边在A2B3右侧作等边三角形A3A2B3,……则点A2019的纵坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
先根据题意得出B1(0,1),OB1=1,如图,过A1作A1A⊥OB1于A,再得出A1的纵坐标为![]() =
=![]() ,再利用含30度角的直角三角形性质得出A1B2=2A1B1=2,过A2作A2B⊥A1B2于B,得出A2的纵坐标为
,再利用含30度角的直角三角形性质得出A1B2=2A1B1=2,过A2作A2B⊥A1B2于B,得出A2的纵坐标为![]() +1=
+1=![]() ,依次类推得出A2019的纵坐标.
,依次类推得出A2019的纵坐标.
解:∵直线l:y=![]() 与y轴交于点B1,
与y轴交于点B1,
∴B1(0,1),OB1=1.
如图,过A1作A1A⊥OB1于A,则OA=![]() OB1=
OB1=![]() ,
,
即A1的纵坐标为![]() =
=![]() .
.
设直线l与x轴交于点M,则∠OMB1=60°,
∴∠OB1M=30°,
∵∠OB1A1=60°,
∴∠A1B1B2=90°,
又∵∠A1B2B1=∠OB1M=30°,
∴A1B2=2A1B1=2,
过A2作A2B⊥A1B2于B,则A1B=![]() A1B2=1,
A1B2=1,
即A2的纵坐标为![]() +1=
+1=![]() ,
,
过A3作A3C⊥A2B3于C,
同理可得,A2B3=2A2B2=4,A2C=![]() A2B3=2,
A2B3=2,
即A3的纵坐标为![]() +1+2=
+1+2=![]() ,
,
同理可得,A4的纵坐标为![]() +1+2+4=
+1+2+4=![]() ,
,
由此可得,An的纵坐标为![]() ,
,
∴点A2019的纵坐标是![]() ,
,
故选:B.


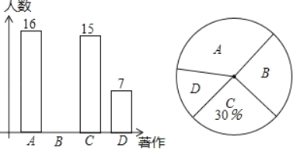
【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:


根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?