题目内容
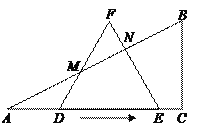
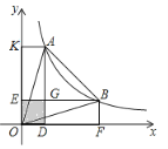
【题目】如图，A，B是反比例函数y＝
（x＞0）图象上的两点，分别过A，B两点向x轴，y轴作垂线段，AD，BE两垂线段交于点G．若图中阴影部分的面积为3，则△OAB的面积为（ ）
A.9B.10C.11D.12
【答案】D
【解析】
首先根据反比例函数图象上的点与坐标轴、向坐标轴作垂线所围成的矩形面积等于|k|，利用阴影部分的面积为3，推导出线段比例关系，比例关系转化为求矩形OFPK的面积，用割补法可求△OAB的面积．
解： 
设FB与KA的延长线相交于点P，
HM垂直平分EK，
∵A，B是反比例函数y＝
（x＞0）图象上的两点，
A点向x轴，y轴作垂线段分别是AD、AK
∴s矩形ODAK＝|k|＝9
同理：s矩形OFBE＝9
∵s矩形ODGE＝3
∴s矩形DFBG＝s矩形EGAK＝9﹣3＝6
∵HM垂直平分EK
∴OE＝EH＝HK
∴s矩形OFPK＝3s矩形OFBE＝3×9＝27
且s矩形AGBP＝2s△ABP＝12
即s△ABP＝6
∴s△AOB＝S矩OFPK-S△AOK -S△OFB-S△ABP＝27﹣6﹣9＝12
故选：D．
练习册系列答案
高中必刷题系列答案
相关题目
