题目内容
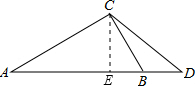
如图，Rt△ABC中，∠ACB=90°，∠A=30°，D为AB的延长线上一点，且AB：BD=4：1，则tan∠BDC=______．
过C作CE⊥AD，交AD于点E，可得∠CEB=90°，
∵Rt△ABC中，∠ACB=90°，∠A=30°，
∴∠ABC=60°，BC=
AB，
由AB：BD=4：1，设BD=x，AB=4x，则AD=BD+AB=5x，BC=2x，
在Rt△CEB中，∠ECB=30°，
可得EB=
BC=x，即ED=EB+BD=x+x=2x，
根据勾股定理得：EC=
=
x，
在Rt△CED中，tan∠BDC=
=
=
．
故答案为：
∵Rt△ABC中，∠ACB=90°，∠A=30°，
∴∠ABC=60°，BC=
| 1 |
| 2 |
由AB：BD=4：1，设BD=x，AB=4x，则AD=BD+AB=5x，BC=2x，
在Rt△CEB中，∠ECB=30°，
可得EB=
| 1 |
| 2 |
根据勾股定理得：EC=
| BC2-EB2 |
| 3 |
在Rt△CED中，tan∠BDC=
| EC |
| ED |
| ||
| 2x |
| ||
| 2 |
故答案为：
| ||
| 2 |
练习册系列答案
阅读快车系列答案
相关题目
，且a＞b＞c，蚂蚁究竟沿怎样的路线爬上去，所经过的距离最短？
