Question

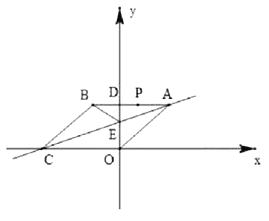
【题目】如图，在平面直角坐标系中，点是原点，四边形是菱形，点的坐标为，点在轴的负半轴上，直线与轴交于点，与轴交于点。

（1）求直线的解析式；

（2）动点从点出发，沿折线方向以1个单位/秒的速度向终点匀速运动，设的面积为，点的运动时间为秒，求与之间的函数关系式。

Answer 1

【答案】（1）；（2）.

【解析】

(1)由点A的坐标，求出OA的长，根据四边形ABCO为菱形，利用菱形的四条边相等得到OC=OA，求出OC的长，即可确定出C的坐标，设直线AC解析式为y=kx+b，将A与C代入求出k与b的值，即可确定出直线AC的解析式；

(2) 对于直线AC解析式，令x=0，得到y的值，即为OE的长，由OD-OE求出DE的长， 当点P在线段AB上时，由P的速度为1个单位/秒，时间为t秒，表示出AP，由AB-AP表示出PB，△PEB以PB为底边，DE为高，表示出S与t的关系式，并求出t的范围即可；当P在线段BC上时，设点E到直线BC的距离h，由P的速度为１个单位/秒，时间为t秒，则 BP的长为t-5，△ABC的面积为菱形面积(OC为底，OD为高)的一半，△AEB的面积以AB为底，DE为高，△BEC以BC为底边，h为高，利用等量关系式，建立方程，解出h的值，△PEB以BP为底边，h为高，表示出S与t的关系式，并求出t的范围即可．

解：（1）∵点的坐标为，

∴，在中，根据勾股定理，

∴，

∵菱形，

∴，

∴，

设直线的解析式为：，

把代入得：

解得，

∴；

（2）令时，得：，则点，

∴，

依题意得：，

①当点在直线上运动时，即

当时，

∴，

②当点在直线上时，即当时，∴；设点E到直线的距离，

∴，

∴，

∴，

∴，

综上得：.

故答案为：（1）；（2）.