题目内容
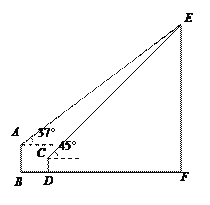
【题目】如图,甲楼AB高20 m,乙楼CD高10 m,两栋楼之间的水平距离BD=20 m,小丽在乙楼楼顶C处观测电视塔塔顶E,测得仰角为45°,求电视塔的高度EF.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ![]() ≈1.4,结果保留整数)
≈1.4,结果保留整数)
【答案】电视塔的高度为110米.
【解析】分析:首先分析题意,根据题意构造直角三角形,分别过点A,C作AM⊥EF,CN⊥EF垂足分别为M、N,在Rt△ECN和Rt△AEM中,借助三角函数解出AM、 CN的值,进而求出电视塔的高度.
详解:如图,分别过点A,C作AM⊥EF,CN⊥EF垂足分别为M、N.
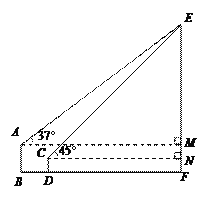
∴MF=AB=20,NF=CD=10.
设EF=x m,则EN=(x―10) m,EM=(x―20) m.
在Rt△ECN中,∠ECN=45°,
∵tan45°=![]() ,
,
∴CN=![]() =
=![]() .
.
在Rt△AEM中,∠EAM=37°,
∵ tan37°=![]() ,
,
∴AM=![]() =
=![]() .
.
又 AM―CN=BD,
∴![]() ―
―![]() =20.
=20.
∴x≈110.
答:电视塔的高度为110米.

练习册系列答案
相关题目