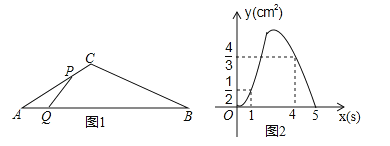题目内容
【题目】定义:数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.
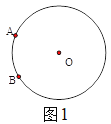
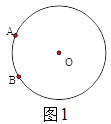
理解:(1)如图![]() ,已知
,已知![]() 是⊙
是⊙![]() 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点![]() ,使
,使![]() 为“智慧三角形”(画出点
为“智慧三角形”(画出点![]() 的位置,保留作图痕迹);
的位置,保留作图痕迹);
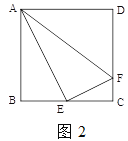
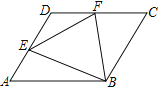
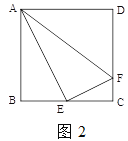
(2)如图![]() ,在正方形
,在正方形![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 上一点,且
上一点,且![]() ,试判断
,试判断![]() 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;
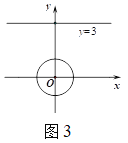
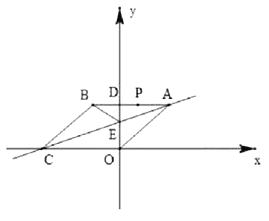
运用:(3)如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,⊙
中,⊙![]() 的半径为
的半径为![]() ,点
,点![]() 是直线
是直线![]() 上的一点,若在⊙
上的一点,若在⊙![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 为“智慧三角形”,其面积的最小值为______.
为“智慧三角形”,其面积的最小值为______.

【答案】![]()
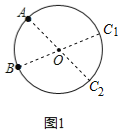
【解析】分析:(1)连结AO并且延长交圆于C1,连结BO并且延长交圆于C2,即可求解;
(2)设正方形的边长为4a,表示出DF、CF以及EC、BE的长,然后根据勾股定理列式表示出AF2、EF2、AE2,再根据勾股定理逆定理判定△AEF是直角三角形,由直角三角形的性质可得△AEF为“智慧三角形”;
(3)根据“智慧三角形”的定义可得△OPQ为直角三角形,根据题意可得一条直角边为1,当斜边最短时,另一条直角边最短,则面积取得最小值,由垂线段最短可得斜边最短为3,根据勾股定理可求另一条直角边,再根据三角形面积可求斜边的高,即点P的横坐标,再根据勾股定理可求点P的纵坐标,从而求解.
详解:(1)如图1所示:
(2)△AEF是否为“智慧三角形”,
理由如下:设正方形的边长为4a,
∵E是DC的中点,
∴DE=CE=2a,
∵BC:FC=4:1,
∴FC=a,BF=4a﹣a=3a,
在Rt△ADE中,AE2=(4a)2+(2a)2=20a2,
在Rt△ECF中,EF2=(2a)2+a2=5a2,
在Rt△ABF中,AF2=(4a)2+(3a)2=25a2,
∴AE2+EF2=AF2,
∴△AEF是直角三角形,
∵斜边AF上的中线等于AF的一半,
∴△AEF为“智慧三角形”;
(3)如图3所示:
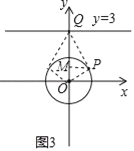
由“智慧三角形”的定义可得△OPQ为直角三角形,
根据题意可得一条直角边为1,当斜边最短时,另一条直角边最短,则面积取得最小值,
由垂线段最短可得斜边最短为3,
由勾股定理可得PQ=![]() ,
,
PM=1×2![]() ÷3=
÷3=![]() ,
,
面积的最小值为: ![]() .
.

 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案