ЬтФПФкШн
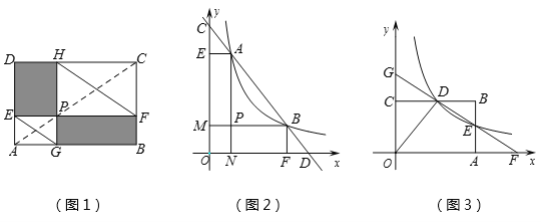
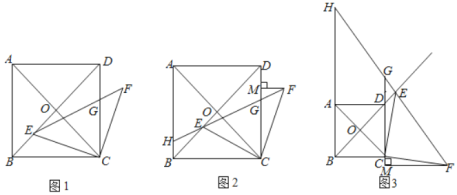
ЁОЬтФПЁПШчЭМЃЌЮЊМгПь5GЭјТчНЈЩшЃЌФГЭЈаХЙЋЫОдквЛИіЦТЖШiЃН1ЃК2.4ЕФЩНЦТABЩЯНЈСЫвЛзљаХКХЫўCDЃЌаХКХЫўЕзЖЫCЕНЩННХAЕФОрРыACЃН13УзЃЌдкОрЩННХAЫЎЦНОрРы18УзЕФEДІЃЌгавЛИпЖШЮЊ10УзЕФНЈжўЮяEFЃЌдкНЈжўЮяЖЅЖЫFДІВтЕУаХКХЫўЖЅЖЫDЕФбіНЧЮЊ37ЁуЃЈаХКХЫўМАЩНЦТЕФЦЪУцКЭНЈжўЮяЕФЦЪУцдкЭЌвЛЦНУцЩЯЃЉЃЌдђаХКХЫўCDЕФИпЖШдМЪЧЃЈЁЁЁЁЃЉЃЈВЮПМЪ§ОнЃКsin37ЁуЁж0.60ЃЌcos37ЁуЁж0.80ЃЌtan37ЁуЁж0.75ЃЉ
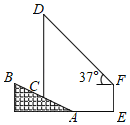
A.22.5УзB.27.5УзC.32.5УзD.45.0Уз
ЁОД№АИЁПB
ЁОНтЮіЁП
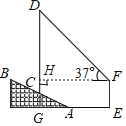
Й§ЕуFзїFHЁЭDCгкЕуHЃЌбгГЄDCНЛEAгкЕуGЃЌПЩЕУЫФБпаЮEFHGЪЧОиаЮЃЌИљОнABЕФЦТЖШiЃН1ЃК2.4ЃЌACЃН13ЃЌПЩЕУCGЃН5ЃЌAGЃН12ЃЌCHЃНGHЉCGЃН10Љ5ЃН5ЃЌдйИљОнШёНЧШ§НЧКЏЪ§МДПЩЧѓГіаХКХЫўCDЕФИпЖШЃЎ
НтЃКШчЭМЃЌЙ§ЕуFзїFHЁЭDCгкЕуHЃЌ
бгГЄDCНЛEAгкЕуGЃЌ
дђЫФБпаЮEFHGЪЧОиаЮЃЌ
ЁрFHЃНGEЃЌCGЃНEFЃЌ
ЁпABЕФЦТЖШiЃН1ЃК2.4ЃЌACЃН13ЃЌ
ЁрCGЃН5ЃЌAGЃН12ЃЌ
ЁрCHЃНGHЉCGЃН10Љ5ЃН5ЃЌ
ЁрGEЃНAG+AEЃН12+18ЃН30ЃЌ
ЁрдкRtЁїDCFжаЃЌЁЯDFCЃН37ЁуЃЌFHЃНGEЃН30ЃЌ
ЁрDHЃНFHtan37ЁуЁж30ЁС0.75Ёж22.5ЃЌ
ЁрCDЃНDH+CHЁж22.5+5Ёж27.5ЃЈУзЃЉЃЎ
ЫљвдаХКХЫўCDЕФИпЖШдМЪЧ27.5УзЃЎ
ЙЪбЁЃКBЃЎ

ЁОЬтФПЁПЧЖЋФЯжнФГГЌЪаЙКНјМзЁЂввСНжжЩЬЦЗЃЌвбжЊЙКНј3МўМзЩЬЦЗКЭ2МўввЩЬЦЗЃЌаш60дЊЃЛЙКНј2МўМзЩЬЦЗКЭ3МўввЩЬЦЗЃЌаш65дЊЃЎ
ЃЈ1ЃЉМзЁЂввСНжжЩЬЦЗЕФНјЛѕЕЅМлЗжБ№ЪЧЖрЩйЃП
ЃЈ2ЃЉЩшМзЩЬЦЗЕФЯњЪлЕЅМлЮЊxЃЈЕЅЮЛЃКдЊ/МўЃЉЃЌдкЯњЪлЙ§ГЬжаЗЂЯжЃКЕБ11ЁмxЁм19ЪБЃЌМзЩЬЦЗЕФШеЯњЪлСПyЃЈЕЅЮЛЃКМўЃЉгыЯњЪлЕЅМлxжЎМфДцдквЛДЮКЏЪ§ЙиЯЕЃЌxЁЂyжЎМфЕФВПЗжЪ§жЕЖдгІЙиЯЕШчБэЃК
ЯњЪлЕЅМлxЃЈдЊ/МўЃЉ | 11 | 19 |
ШеЯњЪлСПyЃЈМўЃЉ | 18 | 2 |
ЧыаДГіЕБ11ЁмxЁм19ЪБЃЌyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЩшМзЩЬЦЗЕФШеЯњЪлРћШѓЮЊwдЊЃЌЕБМзЩЬЦЗЕФЯњЪлЕЅМлxЃЈдЊ/МўЃЉЖЈЮЊЖрЩйЪБЃЌШеЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП