Question

【题目】如图

（1）方法体验：

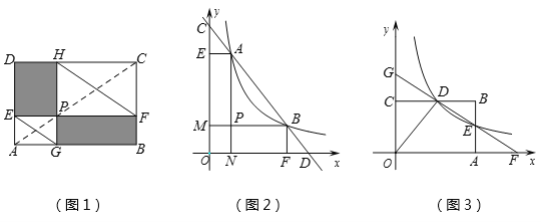
如图1，点P在矩形ABCD的对角线AC上，且不与点A，C重合，过点P分别作边AB，AD的平行线，交两组对边于点E，F和G，H，容易证明四边形PEDH和四边形PFBG是面积相等的矩形，分别连结EG，FH．

①根据矩形PEDH和矩形PFBG面积相等的关系，那么PE·PH= ．

②求证：EG∥FH．

（2）方法迁移：

如图2，已知直线 分别与x轴，y轴交于D，C两点，与双曲线 交于A，B两点． 求证：AC=BD．

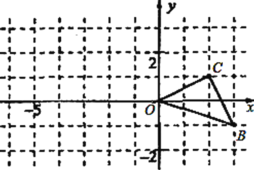
（3）知识应用：

如图3，反比例函数 （x＞0）的图象与矩形ABCO的边BC交于点D,与边AB交于点E, 直线DE与x轴，y轴分别交于点F，G ．若矩形ABCO的面积为10，△ODG与△ODF的面积比为3：5，则k=________．

Answer 1

【答案】（1）①PGPF；②证明见解析；（2）证明见解析；（3）6

【解析】

（1）①矩形PEDH的面积为：PH·PE；矩形PFBG的面积为：PF·PG，由此可得结果；

②PH·PE= PF·PG，可得，可得△EPG∽△FPH，得∠PEG=∠PFH，证得结果；

（2）由k的几何意义，得四边形MPAE的面积=四边形NPBF的面积，可证△APB∽△NPM，MNAB，得四边形ACMN与四边形DBMN均是平行四边形，证得结果；

（3）作DHOA，由面积比得到GD：DF=3:5，由（2）的GD=EF，进一步得到GD，DE，EF的比例关系，设出D（），用DHOGAB，表示出AO，AB的长度，利用矩形面积求出k．

（1）①由图知：矩形PEDH的面积为：PH·PE；矩形PFBG的面积为：PF·PG，

故答案为：PGPF；

②解：∵PEPH= PGPF

∴ 又∵∠EPG=∠HPF=90°

∴△EPG∽△FPH

∴∠PEG=∠PFH

∴EG∥FH

(方法二，如图，记FH，EG与AC交与M，N,

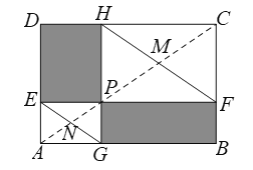
则PM=MH，PN=NG,

∴∠MPH=∠MHP, ∠NPG=∠NGP,

又∵∠NPG=∠MPH，

∴∠MHP=∠NGP

∴EG∥FH

（2）解：先利用四边形OEAN的面积=四边形OFBM的面积=k的绝对值；

∴四边形MPAE的面积=四边形NPBF的面积

∴ 即

又∵∠APB=∠NPM=90°

∴△APB∽△NPM

∴∠ABP=∠PMN

∴MN∥AB

易得四边形ACMN与四边形DBMN均是平行四边形

∴AC=MN=BD

（3）作DHOA于H

∵△ODG与△ODF的面积比为3：5

∴

设，则

由（2）知：

设D（），即

由，得，即

又，得

∴

∴

∴，解得．