题目内容
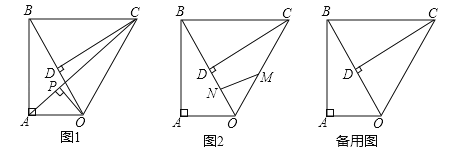
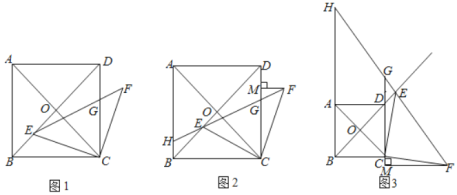
【题目】如图1,在正方形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,点
,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,将
,将![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)若![]() ,求
,求![]() 的面积;
的面积;
(2)如图2,线段![]() 的延长线交
的延长线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,点![]() 为射线
为射线![]() 上一点,线段
上一点,线段![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 垂直直线
垂直直线![]() 于点
于点![]() ,请直接写出线段
,请直接写出线段![]() 的数量关系.
的数量关系.
【答案】(1)5;(2)见解析;(3)![]()
【解析】
(1)如图1中,利用勾股定理计算CE的长,由旋转可知△CEF是等腰直角三角形,可得结论;
(2)如图2,过E作EN⊥AB于N,作EP⊥BC于P,证明△CPE≌△CMF(AAS),得EP=FM,由角平分线的性质得EP=EN=FM,证明△NHE≌△MGF(AAS),得NH=MG,由△BEN是等腰直角三角形,得BN=![]() BE,最后由线段的和可得结论;
BE,最后由线段的和可得结论;
(3)如图3,构建辅助线,构建全等三角形,证明△CPE≌△FMC(AAS),得EP=CM,PC=FM,由△DPE是等腰直角三角形,得PE=PD,证明△HNE≌△GMF(AAS),由△BEN是等腰直角三角形,得BN=![]() BE,同理可得结论.
BE,同理可得结论.
(1)在正方形![]() 中,
中,![]()
![]()
![]()
![]()
![]()
(2)过点![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]()
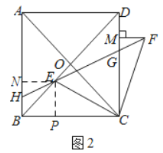
![]()
![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 是等腰直角三角形
是等腰直角三角形
![]()
![]()
(3)BH﹣MG=![]() BE,理由是:
BE,理由是:
如图3,过E作EN⊥AB于N,交CG于P,
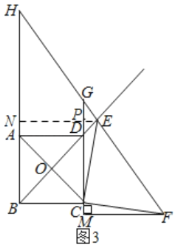
∵EP⊥BC,FM⊥CD,AB∥CD,
∴EP⊥CD,
∴∠EPC=∠FMC=90°,
∵∠M=∠ECF=90°,
∴∠ECP+∠FCM=∠FCM+∠CFM=90°,
∴∠ECP=∠CFM,
∵CE=CF,
∴△CPE≌△FMC(AAS),
∴PC=FM,
∵△DPE是等腰直角三角形,
∴PE=PD,
∴EN=BN=PN+PE=BC+PE=CD+PD=PC=FM,
∵AB∥CD,
∴∠H=∠FGM,
∵∠ENH=∠M=90°,
∴△HNE≌△GMF(AAS),
∴NH=MG,
∴BH﹣MG=BH﹣NH=BN,
∵△BEN是等腰直角三角形,
∴BN=![]() BE,
BE,
∴BH﹣MG=![]() BE.
BE.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案【题目】某校为提高学生体考成绩,对全校300名九年级学生进行一分种跳绳训练.为了解学生训练效果,学校体育组在九年级上学期开学初和学期末分别对九年级学生进行一分种跳绳测试,学生成绩均为整数,满分20分,大于18分为优秀.现随机抽取了同一部分学生的两次成绩进行整理、描述和分析.(成绩得分用x表示,共分成五组:A.x<13,B.13≤x<15,C.15≤x<17,D.17≤x<19,E.19≤x≤20)
开学初抽取学生的成绩在D组中的数据是:17,17,17,17,17,18,18.
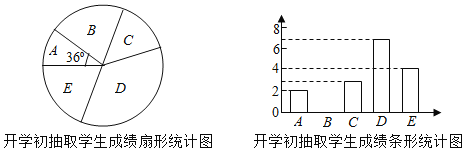
学期末抽取学生成绩统计表
学生成绩 | A组 | B组 | C组 | D组 | E组 |
人数 | 0 | 1 | 4 | 5 | a |
分析数据:
平均数 | 中位数 | 众数 | |
开学初抽取学生成绩 | 16 | b | 17 |
学期末抽取学生成绩 | 18 | 18.5 | 19 |
根据以上信息,解答下列问题:
(1)直接写出图表中a、b的值,并补全条形统计图;
(2)假设该校九年级学生都参加了两次测试,估计该校学期末成绩优秀的学生人数比开学初成绩优秀的学生人数增加了多少?
(3)小莉开学初测试成绩16分,学期末测试成绩19分,根据抽查的相关数据,请选择一个合适的统计量评价小莉的训练效果.