题目内容
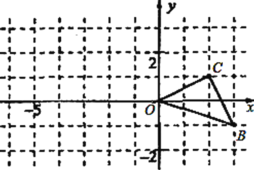
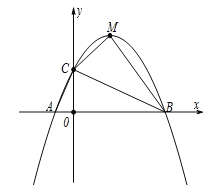
【题目】如图,已知抛物线![]() 交x轴于A、B两点(点A在点B的左侧),与y轴交于点C.
交x轴于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求点A、B、C的坐标;
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积;
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)A(-1,0)、B(5,0)、C(0,2);(2)6;(3)存在![]() 、
、![]() 、
、![]() 三点,它们的坐标分别是
三点,它们的坐标分别是![]() (-1-
(-1-![]() ,0),
,0),![]() (
(![]() -1,0),
-1,0),![]() (
(![]() ,0),
,0),![]() .
.
【解析】
(1)令y=0求A、B两点横坐标,令x=0求C点纵坐标;
(2)由抛物线顶点坐标公式求M点坐标,过M作MN垂直y轴于N,根据S△BCM=SOBMN-S△OBC-S△MNC求△BCM的面积;
(3)根据AC为腰,AC为底两种情况求P点坐标.当AC为腰时,分为A为等腰三角形的顶点,C为等腰三角形的顶点,两种情况求P点坐标;当AC为底时,作线段AC的垂直平分线交x轴于P点,利用三角形相似求OP.
解:(1)令![]() x2+
x2+![]() x+2=0,
x+2=0,
解得:![]() =-1,
=-1,![]() =5,
=5,
令x=0,则y=2,
∴A、B、C的坐标分别是:A(-1,0)、B(5,0)、C(0,2);
(2)∵![]()
∴顶点M的坐标是M(2,![]() ),
),
过M作MN垂直y轴于N,
∴△BCM的面积=![]() -
-![]() -
-![]()
=![]() (2+5)×
(2+5)×![]() -
-![]() ×5×2-
×5×2-![]() ×(
×(![]() -2)×2=6;
-2)×2=6;
(3)存在
当以AC为腰时,在x轴上有两个点分别为![]() ,
,![]() ,
,
∵![]()
则![]() =1+
=1+![]() ,
,![]() =
=![]() -1,
-1,
∴![]() ,
,![]() 的坐标分别是:
的坐标分别是:![]() (-1-
(-1-![]() ,0),
,0),![]() (
(![]() -1,0);
-1,0);
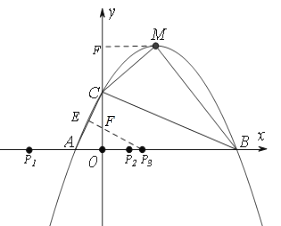
当以AC为底时,作AC的垂直平分线交x轴于![]() ,交y轴于F,垂足为E,
,交y轴于F,垂足为E,
∴CE=![]() ,
,
易证△CEF∽△COA,
∴![]() ,
,
∴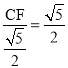 ,
,
∴CF=![]() ,
,
∴OF=OC-CF=2-![]() =
=![]() ,
,
∴EF=![]()
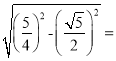
![]()
又△CEF∽△![]() OF,
OF,
∴![]() ,
,
∴![]() ,
,
则![]() 的坐标为
的坐标为![]() (
(![]() ,0);
,0);
当以AC为腰时,点C为顶点时,有AC=PC,
则点P4为(1,0);
∴存在![]() 、
、![]() 、
、![]() 三点,它们的坐标分别是:
三点,它们的坐标分别是:
![]() (-1-
(-1-![]() ,0),
,0),![]() (
(![]() -1,0),
-1,0),![]() (
(![]() ,0),
,0),![]() ;
;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】李辉到服装专卖店去做社会调查,了解到商店为了激励营业员的工作积极性实行了“月总收入=基本工资+计件奖金”的方法,并获得了如下信息:
营业员 | 嘉琪 | 嘉善 |
月销售件数/件 | 400 | 300 |
月总收入/元 | 7800 | 6600 |
假设月销售件数为x件,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)求a、b的值.
(2)若营业员嘉善某月总收入不低于4200元,那么嘉善当月至少要卖多少件衣服?