题目内容
如图,
(1)图中将两个等宽矩形重叠一起,则重叠四边形ABCD是什么特殊四边形?请说明理由;
(2)若(1)中是两个全等的矩形,矩形的长为8cm,宽为4cm,重叠一起时不完全重合,试求重叠四边形ABCD的最小面积和最大面积,并请对面积最大时的情况画出示意图.
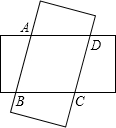
(1)图中将两个等宽矩形重叠一起,则重叠四边形ABCD是什么特殊四边形?请说明理由;
(2)若(1)中是两个全等的矩形,矩形的长为8cm,宽为4cm,重叠一起时不完全重合,试求重叠四边形ABCD的最小面积和最大面积,并请对面积最大时的情况画出示意图.

(1)重叠四边形ABCD是菱形.
证明:根据矩形对边平行,可得ABCD是平行四边形;
因为矩形等宽,即ABCD各边上的高相等.
根据平行四边形的面积公式可得邻边相等,
所以ABCD是菱形.
(2)当菱形ABCD为正方形时,s最小=42=16(cm2);
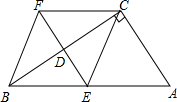
当菱形ABCD如图时,面积最大.
设CD=x,根据勾股定理得x2=(8-x)2+42,
解得x=5.
∴s最大=BC×DE=5×4=20(cm2).
证明:根据矩形对边平行,可得ABCD是平行四边形;
因为矩形等宽,即ABCD各边上的高相等.
根据平行四边形的面积公式可得邻边相等,
所以ABCD是菱形.
(2)当菱形ABCD为正方形时,s最小=42=16(cm2);

当菱形ABCD如图时,面积最大.
设CD=x,根据勾股定理得x2=(8-x)2+42,
解得x=5.
∴s最大=BC×DE=5×4=20(cm2).

练习册系列答案
相关题目