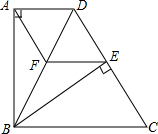
题目内容
已知,如图,正方形ABCD,菱形EFGP,点E、F、G分别在AB、AD、CD上,延长DC,PH⊥DC于H.
(1)求证:GH=AE;
(2)若菱形EFGP的周长为20cm,cos∠AFE=
,FD=2,求△PGC的面积.

(1)求证:GH=AE;
(2)若菱形EFGP的周长为20cm,cos∠AFE=
| 4 |
| 5 |

(1)证明:由菱形性质知:∠EFG+∠FGP=180°,EF=GP=EP=FG,
又∠AEF+∠AFE=90°,∠DFG+∠DGF=90°,∠AFE+∠EFG+∠DFG=180°,∠DGF+∠FGP+∠PGH=180°,
∴∠AFE=∠GPH,
又∵∠A=∠H,
∴△AEF≌△HGP,(AAS)
∴GH=AE;
(2)∵菱形EFGP的周长为20cm,
∴EF=GP=EP=FG=5cm,
又∵cos∠AFE=
,
∴在△AEF中,AF=4,EF=5,
又∵FD=2,
∴正方形边长=AD=DC=6,
在△DFG中,DG=
=
,
∴GC=6-
,
又由(1)知PH=AF,
∴△PGC的面积=
×GC×PH=
×GC×AF=12-2
(cm2).
又∠AEF+∠AFE=90°,∠DFG+∠DGF=90°,∠AFE+∠EFG+∠DFG=180°,∠DGF+∠FGP+∠PGH=180°,
∴∠AFE=∠GPH,
又∵∠A=∠H,
∴△AEF≌△HGP,(AAS)
∴GH=AE;
(2)∵菱形EFGP的周长为20cm,
∴EF=GP=EP=FG=5cm,
又∵cos∠AFE=
| 4 |
| 5 |
∴在△AEF中,AF=4,EF=5,
又∵FD=2,
∴正方形边长=AD=DC=6,
在△DFG中,DG=
| FG2-DF2 |
| 21 |
∴GC=6-
| 21 |
又由(1)知PH=AF,
∴△PGC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 21 |

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目