Question

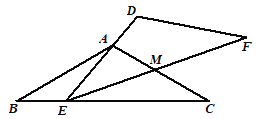
【题目】在ABCD中，SABCD=24，AE平分∠BAC，交BC于E，沿AE将△ABE折叠，点B的对应点为F，连接EF并延长交AD于G，EG将ABCD分为面积相等的两部分．则S△ABE= ．

Answer 1

【答案】4
【解析】解：根据题意，AE平分∠BAC，交BC于E，沿AE将△ABE折叠，点B的对应点为F， ∴点F在对角线AC上，且S△ABE=S△AFE ．
∵EG将ABCD分为面积相等的两部分，
∴点F为对角线AC的中点．
∴S△AFE=S△CFE（等底同高）．
∵S平行四边形ABCD=24，
∴S△ABE=S△AFE=S△CFE= S△ABC= S平行四边形ABCD=4．
故答案是：4．

【考点精析】通过灵活运用平行四边形的性质和翻折变换（折叠问题），掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等即可以解答此题．