题目内容
【题目】如图,已知抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B两点,与y轴交于C点,其对称轴为直线x=1.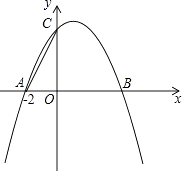
(1)直接写出抛物线的解析式:;
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形?若存在,求出E、F的坐标;若不存在,请说明理由.
【答案】
(1)y=﹣ ![]() x2+x+4
x2+x+4
(2)
解:由抛物线y=﹣ ![]() x2+x+4可知C(0,4),
x2+x+4可知C(0,4),
∵抛物线的对称轴为直线x=1,根据对称性,
∴C′(2,4),
∴A′(0,0)
(3)
解:存在.
设F(x,﹣ ![]() x2+x+4).
x2+x+4).
以A、C、E、F为顶点的四边形为平行四边形,
①若AC为平行四边形的边,如答图1﹣1所示,则EF∥AC且EF=AC.
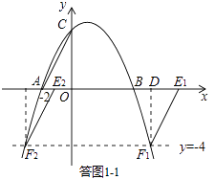
过点F1作F1D⊥x轴于点D,则易证Rt△AOC≌Rt△E1DF1,
∴DE1=2,DF1=4.
∴﹣ ![]() x2+x+4=﹣4,
x2+x+4=﹣4,
解得:x1=1+ ![]() ,x2=1﹣
,x2=1﹣ ![]() .
.
∴F1(1+ ![]() ,﹣4),F2(1﹣
,﹣4),F2(1﹣ ![]() ,﹣4);
,﹣4);
∴E1(3+ ![]() ,0),E2(3﹣
,0),E2(3﹣ ![]() ,0).
,0).
②若AC为平行四边形的对角线,如答图1﹣2所示.
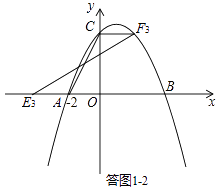
∵点E3在x轴上,∴CF3∥x轴,
∴点C为点A关于x=1的对称点,
∴F3(2,4),CF3=2.
∴AE3=2,
∴E3(﹣4,0),
综上所述,存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形;
点E、F的坐标为:E1(3+ ![]() ,0),F1(1+
,0),F1(1+ ![]() ,﹣4);E2(3﹣
,﹣4);E2(3﹣ ![]() ,0),F2(1﹣
,0),F2(1﹣ ![]() ,﹣4);E3(﹣4,0),F3(2,4)
,﹣4);E3(﹣4,0),F3(2,4)
【解析】解:(1)∵A(﹣2,0),对称轴为直线x=1.
∴B(4,0),
把A(﹣2,0),B(4,0)代入抛物线的表达式为:![]() ,
,
解得: 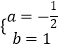 ,
,
∴抛物线的解析式为:y=﹣ ![]() x2+x+4;
x2+x+4;
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案