题目内容
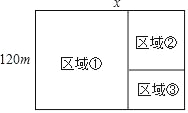
【题目】如图所示,某校在开发区一块宽为120m的矩形用地上新建分校区,规划图纸上把它分成①②③三个区域,区域①和区域②为正方形,区域①为教学区;区域②为生活区;区域③为活动区,设这块用地长为xm,区域③的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)若区域③的面积为3200m2,那么这块用地的长应为多少?
【答案】(1)y=﹣x2+360x﹣28800,其中120<x<240;(2)这块用地的长应为200m或160m
【解析】分析:(1)由题意可知:区域②的边长为(x﹣120)m,则区域③的长为(x﹣120)m,宽为(240﹣x)m,根据题意给出的等量关系即可求出答案.
(2)令y=3200,解一元二次方程即可求出答案.
详解:(1)由题意可知:区域②的边长为(x﹣120)m,则区域③的长为(x﹣120)m,宽为(240﹣x)m,那么y=(240﹣x)(x﹣120)=﹣x2+360x﹣28800,其中120<x<240;
(2)由题意可知:﹣x2+360x﹣28800=3200.
∵x2﹣360x+32000=0,
解得:x=200或x=160,
∴这块用地的长应为200m或160m.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目