题目内容
【题目】如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC. 
(1)求证:AP是⊙O的切线;
(2)求PD的长.
【答案】
(1)证明:连接OA.
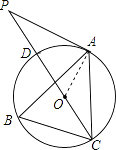
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠ACP=∠CAO=30°,
∴∠AOP=60°,
∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=90°,
∴OA⊥AP,
∴AP是⊙O的切线,
(2)解:连接AD.
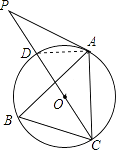
∵CD是⊙O的直径,
∴∠CAD=90°,
∴AD=ACtan30°=3× ![]() =
= ![]() ,
,
∵∠ADC=∠B=60°,
∴∠PAD=∠ADC﹣∠P=60°﹣30°=30°,
∴∠P=∠PAD,
∴PD=AD= ![]() .
.
【解析】(1)首先连接OA,由∠B=60°,利用圆周角定理,即可求得∠AOC的度数,又由OA=OC,即可求得∠OAC与∠OCA的度数,利用三角形外角的性质,求得∠AOP的度数,又由AP=AC,利用等边对等角,求得∠P,则可求得∠PAO=90°,则可证得AP是⊙O的切线;(2)由CD是⊙O的直径,即可得∠DAC=90°,然后利用三角函数与等腰三角形的判定定理,即可求得PD的长.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目