题目内容
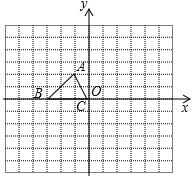
【题目】在解决线段数量关系问题中,如果条件中有角平分线,经常采用下面构造全等三角形的解决思路.如:在图1中,若![]() 是
是![]() 的平分线
的平分线![]() 上一点,点
上一点,点![]() 在
在![]() 上,此时,在
上,此时,在![]() 截取
截取![]() ,连接
,连接![]() ,根据三角形全等的判定
,根据三角形全等的判定![]() ,容易构造出全等三角形⊿
,容易构造出全等三角形⊿![]() 和⊿
和⊿![]() ,参考上面的方法,解答下列问题:
,参考上面的方法,解答下列问题:

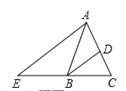
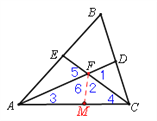
如图2,在非等边⊿![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() 的平分线,且
的平分线,且![]() 交于点
交于点![]() .求证:
.求证: ![]() .
.

【答案】详见解析.
【解析】试题分析:本题要直接证明![]() ,可以参照阅读材料提供的方法在长边
,可以参照阅读材料提供的方法在长边![]() 上截取一条来等于
上截取一条来等于![]() 中的其中一条,通过构造出的全等三角形来使问题得以解决.
中的其中一条,通过构造出的全等三角形来使问题得以解决.
试题解析:在边![]() 上截取
上截取![]() ,
,
∵![]() 分别是
分别是![]() 的平分线,
的平分线,
∴![]() .
.
在![]()
![]() 和
和![]()
![]() 中
中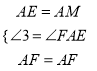
∴![]()
![]() ≌
≌![]()
![]()
![]() .
.
∴![]() .
.
∵![]() .
.
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() .
.
∴![]() .
.
∴![]() .
.
在![]()
![]() 和
和![]()
![]() 中
中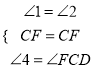
∴![]()
![]() ≌
≌![]()
![]()
![]() .
.
∴![]() .
.
∵![]() ∴
∴![]() 即
即![]() .
.

练习册系列答案
相关题目