题目内容
【题目】小南身高为163cm，一张纸的厚度为0.09mm，现将这张纸连续对折(假设对折始终能成功),若连续对折
次后,纸的厚度超过了小南的身高,那么的值最小是
A. 12 B. 13 C. 14 D. 15
【答案】D
【解析】
一张纸的厚度为0.09mm，对折1次后纸的厚度为0.09×2mm；
对折2次后纸的厚度为0.09×2×2=0.09×22mm；
对折3次后纸的厚度为0.09×23mm；
对折n次后纸的厚度为0.09×2nmm，据此列出方程．即可求解．
解：一张纸的厚度为0.09mm，对折1次后纸的厚度为0.09×2mm；
对折2次后纸的厚度为0.09×2×2=0.09×22mm；
对折3次后纸的厚度为0.09×23mm；
对折n次后纸的厚度为0.09×2nmm
根据题意可得： 0.09×2n
1.63×1000，
解得2n18111.111…．
而214＜18111.111…＜215，
因而n最小值是15．
故选：D．
练习册系列答案
相关题目
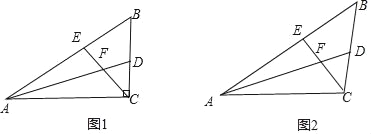
【题目】图1是用绳索织成的一片网的一部分，小明探索这片网的结点数（V），网眼数（F），边数（E）之间的关系，他采用由特殊到一般的方法进行探索，列表如下：
特殊网图 |
|
|
|
|
结点数（V） | 4 | 6 | 9 | 12 |
网眼数（F） | 1 | 2 | 4 | 6 |
边数（E） | 4 | 7 | 12 | ☆ |
表中“☆”处应填的数字为_____；根据上述探索过程，可以猜想V，F，E之间满足的等量关系为_____；
如图2，若网眼形状为六边形，则V，F，E之间满足的等量关系为___ ．
