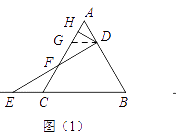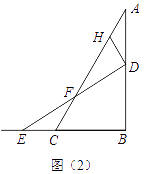题目内容
【题目】如图,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,当△EDC旋转到A,D,E三点共线时,线段BD的长为 . 
【答案】4 ![]() 或
或 ![]()
【解析】解:①如图1, 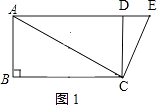 ,
,
∵AC= ![]() =4
=4 ![]() ,CD=4,CD⊥AD,
,CD=4,CD⊥AD,
∴AD= ![]() =
= ![]() =
= ![]() =8,
=8,
∵AD=BC,AB=DC,∠B=90°,
∴四边形ABCD是矩形,
∴BD=AC=4 ![]() .
.
②如图2,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,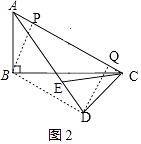 ,
,
∵AC=4 ![]() ,CD=4,CD⊥AD,
,CD=4,CD⊥AD,
∴AD= ![]() =
= ![]() =8,
=8,
∵点D、E分别是边BC、AC的中点,
∴DE= ![]() AB=2,
AB=2,
∴AE=AD﹣DE=8﹣2=6,
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵ ![]() =
= ![]() ,
,
∴△ECA∽△DCB,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BD= ![]() =
= ![]() .
.
综上所述,BD的长为4 ![]() 或
或 ![]() ,
,
故答案为:4 ![]() 或
或 ![]() .
.
分两种情况分析,A、D、E三点所在直线与BC不相交和与BC相交,然后利用勾股定理分别求解即可求得答案.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
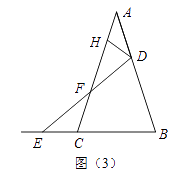
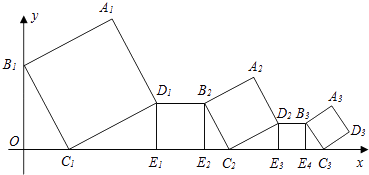
【题目】图1是用绳索织成的一片网的一部分,小明探索这片网的结点数(V),网眼数(F),边数(E)之间的关系,他采用由特殊到一般的方法进行探索,列表如下:
特殊网图 |
|
|
|
|
结点数(V) | 4 | 6 | 9 | 12 |
网眼数(F) | 1 | 2 | 4 | 6 |
边数(E) | 4 | 7 | 12 | ☆ |
表中“☆”处应填的数字为_____;根据上述探索过程,可以猜想V,F,E之间满足的等量关系为_____;
如图2,若网眼形状为六边形,则V,F,E之间满足的等量关系为___ .