题目内容
【题目】如图,大楼AB高16m,远处有一塔CD,某人在楼底B处测得塔顶C的仰角为38.5°,在楼顶A处测得塔顶的仰角为22°,求塔高CD的高及大楼与塔之间的距离BC的长.
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,si38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80).

【答案】40米
【解析】试题分析:过点A作AE⊥CD于点E,由题意可知: ![]()
![]() ED=AB=16米,设大楼与塔之间的距离BD的长为x米,则AE=BD=x,分别在Rt△BCD中和Rt△ACE中,用
ED=AB=16米,设大楼与塔之间的距离BD的长为x米,则AE=BD=x,分别在Rt△BCD中和Rt△ACE中,用![]() 表示出
表示出![]() 和
和![]() ,利用CDCE=DE,得到有关
,利用CDCE=DE,得到有关![]() 的方程求得
的方程求得![]() 的值即可.
的值即可.
试题解析:过点A作AE⊥CD于点E,由题意可知: ![]() ED=AB=16米
ED=AB=16米
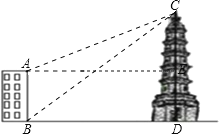
设大楼与塔之间的距离BD的长为x米,则AE=BD=x(不设未知数x也可以)
∵在Rt△BCD中, ![]()
∴![]()
∵在Rt△ACE中, ![]()
∴![]()
∵CDCE=DE,
∴0.8x0.4x=16,
∴x=40,
即BD=40(米),
CD=0.8×40=32(米),
答:塔高CD是32米,大楼与塔之间的距离BD的长为40米.

【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×2.112-4×2.11×2.22+2.222”,她觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
(1)填写下表:
x=-1,y=1 | x=1,y=0 | x=3,y=2 | x=2,y=-1 | x=2,y=3 | |
A=2x-y | -3 | 2 | 4 | 5 | 1 |
B=4x2-4xy+y2 | 9 | 4 | 16 |
(2)观察表格,你发现A与B有什么关系?
解决问题:
(3)请利用A与B之间的关系计算:4×2.112-4×2.11×2.22+2.222.