题目内容
【题目】如图，已知直线a∥b，且a与b之间的距离为4，点A到直线a的距离为2，点B到直线b的距离为3，AB=
．试在直线a上找一点M，在直线b上找一点N，满足MN⊥a且AM+MN+NB的长度和最短，则此时AM+NB=
A．6 B．8 C．10 D．12
【答案】B
【解析】
试题MN表示直线a与直线b之间的距离，是定值，只要满足AM+NB的值最小即可，如图，作点A关于直线a的对称点A′，连接A′B交直线b与点N，过点N作NM⊥直线a，连接AM，
∵A到直线a的距离为2，a与b之间的距离为4，
∴AA′=MN=4。∴四边形AA′NM是平行四边形。
∴AM+NB=A′N+NB=A′B。
由两点之间线段最短，可得此时AM+NB的值最小。
过点B作BE⊥AA′，交AA′于点E，
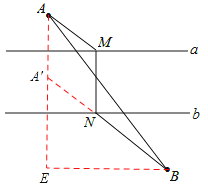
易得AE=2+4+3=9，AB=
，A′E=2+3=5，
在Rt△AEB中，
，
在Rt△A′EB中，
。故选B。
练习册系列答案
阅读快车系列答案
相关题目
