题目内容
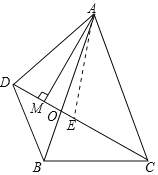
【题目】如图,△ABC中,AB=AC,点D为△ABC外一点,DC与AB交于点O,且∠BDC=∠BAC.

(1)求证:∠ABD=∠ACD;
(2)过点A作AM⊥CD于M,求证:BD+DM=CM.
【答案】见解析
【解析】
(1)由三角形内角和定理即可得出结论;
(2)在CM上截取CE=BD,连接AE,由SAS证明△ABD≌△ACE得出AD=AE,由等腰三角形的性质得出DM=EM,即可得出结论.
(1)证明:∵∠BDC=∠BAC,∠BOD=∠AOC,
∴∠ABD=∠ACD;
(2)证明:在CM上截取CE=BD,连接AE,如图所示:
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),
∴AD=AE,
∵AM⊥CD,
∴DM=EM,
∴BD+DM=CE+EM=CM.

练习册系列答案
相关题目