Question

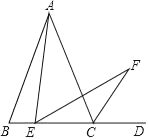
【题目】如图，点B、F、C、E在一条直线上，FB=CE，AB∥ED，AC∥FD;

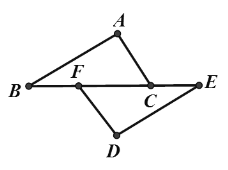
(1)已知∠A=85°,∠ACE=115°,求∠B度数;

(2)求证：AB=DE．

Answer 1

【答案】（1）30°；（2）见解析

【解析】

（1）直接利用三角形的外角性质求解即可；

（2）由平行线的性质可得∠ACB=∠DFE，∠B=∠E，然后根据ASA可证△ABC≌△DEF，进而可得结论．

（1）解：∵∠A=85°，∠ACE=115°，∠B+∠A=∠ACE，

∴∠B=115°－85°=30°；

（2）证明：∵ AC∥FD，AB∥ED，

∴ ∠ACB=∠DFE，∠B=∠E，

∵FB=CE，∴BC=EF，

在△ABC和△DEF中，

，

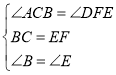∴△ABC≌△DEF(ASA) ，

∴AB=DE．