题目内容
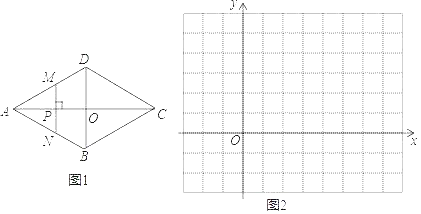
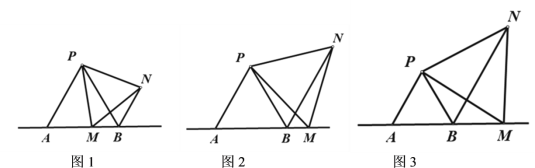
【题目】如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN,
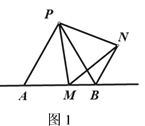
(1)M点如图1的位置时,如果AM=5,求BN的长;
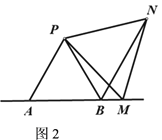
(2)M点在如图2位置时,线段AB、BM、BN三者之间的数量关系__________________;
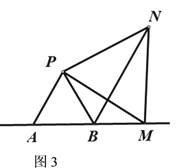
(3)M点在如图3位置时,当BM=AB时,证明:MN⊥AB.
【答案】(1)5;(2)AB+BM=BN;(3)详见解析
【解析】
(1)根据等边三角形的性质可得:∠APB=∠MPN,PA=PB,PM=PN,然后即可利用SAS证明△PAM≌△PBN,再利用全等三角形的性质即得结论;
(2)仿(1)的方法利用SAS证明△PAM≌△PBN,可得AM=BN,进一步即得结论;
(3)根据等边三角形的性质、等腰三角形的性质和三角形的外角性质可得∠BPM=∠PMB =30°,易知∠PMN=60°,问题即得解决.
解:(1)如图1,∵△PAB,△PMN都是等边三角形,
∴∠APB=∠MPN=60°,PA=PB,PM=PN,
∴∠APM=∠BPN,
∴△PAM≌△PBN(SAS) ,
∴AM=BN=5,∴BN的长为5;
(2) AB+BM=BN;
理由:如图2,∵△PAB,△PMN都是等边三角形,
∴∠APB=∠MPN=60°,PA=PB,PM=PN,
∴∠APM=∠BPN,
∴△PAM≌△PBN(SAS) ,
∴AM=BN,即AB+BM=BN;
故答案为:AB+BM=BN;
(3)证明:如图3,∵△PAB是等边三角形,∴AB=PB,∠ABP=60°,
∵BM=AB,∴PB=BM,∴∠BPM=∠PMB,
∵∠ABP=60°,∴∠BPM=∠PMB =30°,
∵△PMN是等边三角形,∴∠PMN=60°,
∴∠AMN=90°,即MN⊥AB.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目