题目内容
【题目】阅读下列材料:数学课上,老师出示了这样一个问题:
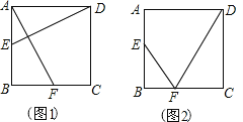
如图1,在等边![]() 中,点
中,点![]() 、
、![]() 在
在![]() 上,且
上,且![]() ,直线
,直线![]() 交
交![]() 于
于![]() 点,交
点,交![]() 延长线于
延长线于![]() 点,且
点,且![]() ,探究线段
,探究线段![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 存在某种数量关系”;
存在某种数量关系”;
小强:“通过观察和度量,发现图1中有一条线段与![]() 相等”;
相等”;
小伟:“通过构造三角形,证明三角形全等,进而可以得到线段![]() 之间的数量关系”.
之间的数量关系”.
……
老师:“保留原题条件,再过点![]() 作
作![]() 交
交![]() 于
于![]() 与
与![]() 相交于点
相交于点![]() (如图2)如果给出
(如图2)如果给出![]() 的值,那么可以求出
的值,那么可以求出![]() 的值”.
的值”.
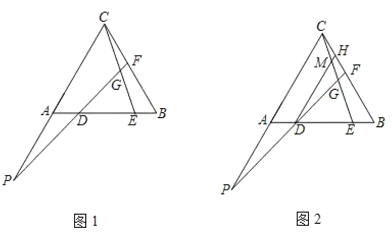
请回答:
(1)在图1中找出![]() 与
与![]() 数量关系,并证明;
数量关系,并证明;
(2)在图1中找出与线段![]() 相等的线段,并证明;
相等的线段,并证明;
(3)探究线段![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(4)若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)![]() ,理由见详解;(2)
,理由见详解;(2)![]() ,理由见详解;(3)
,理由见详解;(3)![]() ,理由见详解;(4)
,理由见详解;(4)![]()
【解析】
(1)先根据三角形内角和定理得:∠BDF+∠DEG=120°,由三角形外角的性质得:∠DEG=60°+∠BCE,代入可得结论;
(2)先判断出△ACD≌△BCE(SAS),得出∠ACD=∠BCE,CD=CE,进而判断出∠ACD=∠P,得CD=DP,即可得出结论;
(3)如图2,作辅助线构建三角形全等,证明![]() ,得
,得![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,由勾股定理得:
,由勾股定理得:![]() ,列方程可得结论;
,列方程可得结论;
(4)如图3,作辅助线,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,证明
,证明![]() ,由
,由![]() 得
得![]() ,
,![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,即
,即![]() ,计算
,计算![]() ,证明
,证明![]() ,可得结论.
,可得结论.
解:(1)如图1,∠BCE+∠BDF=60°,
证明:∵∠DGE=60°,
∴∠BDF+∠DEG=180°﹣60°=120°,
∵△ABC是等边三角形,
∴∠B=60°,
∵∠DEG=∠B+∠BCE,
∴∠BDF+60°+∠BCE=120°,
∴∠BCE+∠BDF=60°;
(2)DP=CE,
证明:如图1,连接CD,

∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AC=BC,
∵AD=BE,
∴△ACD≌△BCE(SAS),
∴∠ACD=∠BCE,CD=CE,
∵∠CAB=∠P+∠ADP=∠P+∠BDF=60°,
由(1)知:∠BDF+∠BCE=60°,
∴∠P=∠BCE=∠ACD,
∴CD=DP,
∴CE=DP;
(3)结论:AD2+ADBD+BD2=CE2,
证明:如图2,在边AC上截取AH=AD,连接DH,过D作DM⊥AC于M,连接CD,
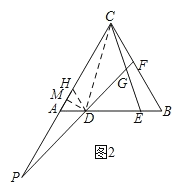
∴∠CAB=60°,
∴△ADH是等边三角形,
∴AD=DH=AH,∠AHD=60°,
∴∠DHC=∠PAD=120°,
由(2)知CD=PD,∠P=∠ACD,
∴△DHC≌△DAP(AAS),
∴CH=AP,
∵AC=AB,AH=AD,
∴AC﹣AH=AB﹣AD,即CH=BD,
∴BD=AP,
Rt△ADM中,∠ADM=30°,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
![]()
![]() ,
,
![]() ;
;
(4)如图3,连接CD,过H作HQ∥DF,交CD于Q,则∠QHD=∠MDG,

设CH=x,FH=y,FG=a,DG=na,CE=CD=ma,
∵DH∥AC,
∴∠DHF=∠ACB=60°,
∵∠CGF=∠DGE=60°,
∴∠DHF=∠CGF,
∵∠DFH=∠CFG,
∴∠MDG=∠MCH,△CGF∽△DHF,
∵DH∥AC,
∴∠CDH=∠ACD=∠GCF=∠MDG=∠QHD,
∴QH=QD,
∵QH∥DF,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,即
,即![]() ,
,
![]()
 ,
,
![]() ,
,
∵∠MCH=∠MDG,∠CMH=∠DMG,
∴△CMH∽△DMG,
![]()
 .
.

 新思维寒假作业系列答案
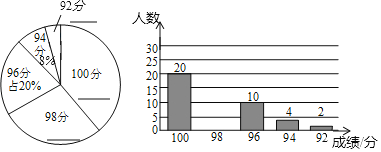
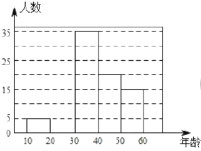
新思维寒假作业系列答案【题目】2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注,某市一研究机构为了了解![]() 岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:
岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |
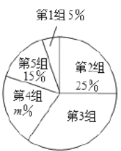
(1)请直接写出![]() 、
、![]() 的值及扇形统计图中第3组所对应的圆心角的度数;
的值及扇形统计图中第3组所对应的圆心角的度数;
(2)请补全上面的频数分布直方图;
(3)假设该市现有![]() 岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少万人?
岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少万人?