Question

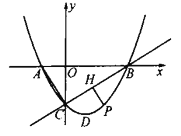
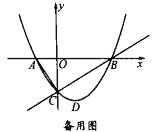
【题目】如图，抛物线与轴分别交于点，，与轴交于点，顶点为，对称轴交轴于点．

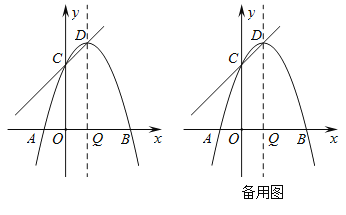
（1）求抛物线的解析式．

（2）若点是抛物线的对称轴上的一点，以点为圆心的圆经过，两点，且与直线相切，求点的坐标．

（3）在抛物线的对称轴上是否存在一点，使得与相似？如果存在，求出点的坐标；如果不存在，请说明理由．

Answer 1

【答案】（1）；（2）点的坐标为或；（3）存在，点的坐标为或

【解析】

（1）由题意把点A、点B的坐标代入抛物线解析式，用待定系数法可得到二次函数的表达式；

（2）根据题意设直线CD切⊙P于点E．连结PE、PA，作CF⊥DQ于点F．通过DF与CF的长，说明△DCF为等腰直角三角形．设点P（1，m），用含m的代数式表示出半径EP、PA的长，根据半径间关系，求出m的值从而确定点P的坐标．

（3）根据题意利用等腰直角三角形，先求出DC和BC的长，由于∠CBQ=∠CDM，若△DCM与△BQC相似，分两种情况，利用比例线段求出满足条件的点M的坐标即可．

解：（1）∵，在抛物线上，

代入，得，

解得

∴抛物线的解析式为．

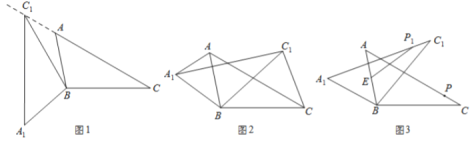
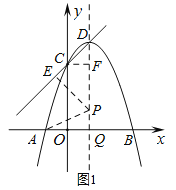
（2）如图1，设直线切于点，连接，，作于点．

∴．

由，得对称轴为直线，，．

∴，，∴，

∴为等腰直角三角形，

∴，

∴，

∵，

∴为等腰直角三角形．

设，则．

在中，，

∴，

∴．

整理，得，

解得．

∴点的坐标为或．

（3）存在点，使得．

如图2，连接，，，

∵，，，

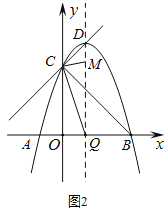
∴为等腰直角三角形，

∴，．

由（2）可知，，

∴．

∴与相似有两种情况，

当时，，解得，

∴．

∴

当时，，解得，

∴，

∴．

综上，点的坐标为或．