Question

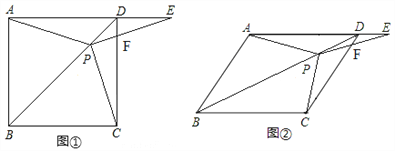
【题目】如图，在边长为4的正方形ABCD中，动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动，动点F以每秒2个单位长度的速度从点B开始沿边BC向点C运动，动点E比动点F先出发1秒，其中一个动点到达终点时，另一个动点也随之停止运动设点F的运动时间为t秒．

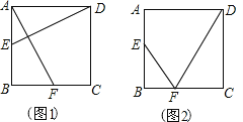
（1）如图1，连接DE，AF．若DE⊥AF，求t的值；

（2）如图2，连结EF，DF．当t为何值时，△EBF∽△DCF？

Answer 1

【答案】（1）t=1；（2）当时，△EBF∽△DCF；

【解析】

（1）利用正方形的性质及条件，得出△ABF≌△DAE，由AE=BF列式计算．

（2）利用△EBF∽△DCF，得出，列出方程求解．

解：（1）∵DE⊥AF，

∴∠AOE=90°，

∴∠BAF+∠AEO=90°，

∵∠ADE+∠AEO=90°，

∴∠BAF=∠ADE，

又∵四边形ABCD是正方形，

∴AB=AD，∠ABF=∠DAE=90°，

在△ABF和△DAE中，

，

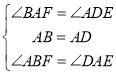∴△ABF≌△DAE（ASA）

∴AE=BF，

∴1+t=2t，

解得t=1；

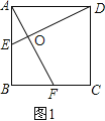
（2）如图2，

∵四边形ABCD是正方形，

∴AB=BC=CD=4，

∵BF=2t，AE=1+t，

∴FC=4-2t，BE=4-1-t=3-t，

当△EBF∽△DCF时，

，

∴=，

解得，t1=，t2=（舍去），

故t=．

所以当t=时，△EBF∽△DCF.