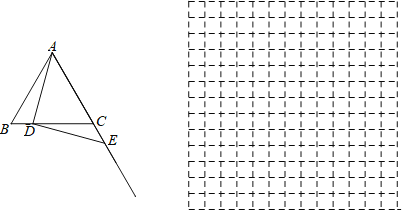题目内容
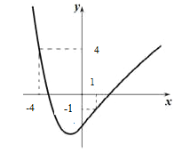
【题目】如图，在平面直角坐标系中抛物线y＝（x+1）（x﹣3）与x轴相交于A、B两点，若在抛物线上有且只有三个不同的点C1、C2、C3，使得△ABC1、△ABC2、△ABC3的面积都等于m，则m的值是（ ）
A. 6 B. 8 C. 12 D. 16
【答案】B
【解析】
根据题目中的函数解析式可以求得该抛物线与x轴的交点坐标和顶点的坐标，再根据在抛物线上有且只有三个不同的点C1、C2、C3，使得△ABC1、△ABC2、△ABC3的面积都等于m，可知其中一点一定在顶点处，从而可以求得m的值．
∵抛物线y=（x+1）（x-3）与x轴相交于A、B两点，
∴点A（-1，0），点B（3，0），该抛物线的对称轴是直线x=
=1，
∴AB=3-（-1）=4，该抛物线顶点的纵坐标是：y=（1+1）×（1-3）=-4，
∵在抛物线上有且只有三个不同的点C1、C2、C3，使得△ABC1、△ABC2、△ABC3的面积都等于m，
∴m=
=8，
故选B．
【题目】一粒木质中国象棋子“兵”，它的正面雕刻一个“兵”字，它的反面是平的
将它从一定高度下掷，落地反弹后可能是“兵”字面朝上，也可能是“兵”字面朝下由于棋子的两面不均匀，为了估计“兵”字面朝上的概率，某实验小组做了棋子下掷实验，实验数据如下表：
实验次数n | 20 | 60 | 100 | 120 | 140 | 160 | 500 | 1000 | 2000 | 5000 |
“兵”字面朝上次数m | 14 | 38 | 52 | 66 | 78 | 88 | 280 | 550 | 1100 | 2750 |
“兵”字面朝上频率 |
|
|
|
|
|
|
|
|
|
|
下面有三个推断：
投掷1000次时，“兵”字面朝上的次数是550，所以“兵”字面朝上的概率是
；
随着实验次数的增加，“兵”字面朝上的频率总在附近，显示出一定的稳定性，可以估计“兵”字面朝上的概率是；
当实验次数为200次时，“兵”字面朝上的频率一定是其中合理的是
A. B. C. 
D. 
【题目】如图，在等边
中，
，点D是线段BC上的一动点，连接AD，过点D作
，垂足为D，交射线AC与点
设BD为xcm，CE为ycm．
小聪根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小聪的探究过程，请补充完整：
通过取点、画图、测量，得到了x与y的几组值，如下表：
| 0 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
|
|
|
| ___ |
| 0 |
|
|
|
| 0 |
说明：补全表格上相关数值保留一位小数
建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
结合画出的函数图象，解决问题：当线段BD是线段CE长的2倍时，BD的长度约为_____cm．
