Question

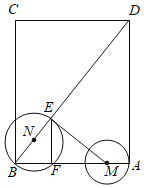
【题目】如图，在矩形ABCD中，AB＝3，BC＝4，半径为1的动圆圆心M从A点出发，沿着AB方向以1个单位长度/每秒的速度匀速运动，同时动点N从点B出发，沿着BD方向也以1个单位长度/每秒的速度匀速运动，设运动的时间为t秒（0≤t≤2.5），以点N为圆心，NB的长为半径的⊙N与BD，AB的交点分别为E，F，连结EF，ME．

（1）①当t＝　 　秒时，⊙N恰好经过点M；②在运动过程中，当⊙M与△ABD的边相切时，t＝　 　秒；

（2）当⊙M经过点B时，①求N到AD的距离；②求⊙N被AD截得的弦长；

（3）若⊙N与线段ME只有一个公共点时，直接写出t的取值范围．

Answer 1

【答案】（1）①，②1或；（2）①，②；（3）0＜t≤或＜t≤

【解析】

（1）①⊙N恰好经过点M即NM=NF=BN，过点N作NG⊥AB于G，连接NF，利用等腰三角形性质即可求得；②⊙M与△ABD的边相切可以有两种情况：⊙M与AD相切或⊙M与BD相切，利用切线性质和相似三角形性质可得结论；

（2）①过点N作NP⊥AD于点P，利用相似三角形性质即可；②由垂径定理可得：GH=2GP，利用勾股定理可求得GP；

（3）⊙N与线段EM只有一个公共点，可以有两种情况：①点M在⊙N的外部，②点M在⊙N的内部．

（1）①如图1，过点N作NG⊥AB于G，连接NF，AM=t，BM=3﹣t，

∵⊙N恰好经过点M

∴点F与M重合，即：BF=BM=3﹣t，

∵NB=NF=t，

∴BG==（3﹣t）

∵矩形ABCD

∴∠BAD=90° AD=BC=4

∴BD===5

∵NG⊥AB

∴∠BGN=90°=∠BAD

∴NG∥AD

∴△BNG∽△BDA

∴==，即5×（3﹣t）=3t，解得：t=

故答案为：

②当⊙M与AD相切时，AM=1，∴t=1

当⊙M与BD相切时，EM⊥BD，且ME=1，∵sin∠ABD===

∴4（3﹣t）=5，解得t=

故答案为：1或；

（2）①过点N作NP⊥AD于点P，当⊙M经过点B时，AM=AB﹣MB=2

∴t=2

∴BN=2，DN=BD﹣BN=3

∵NP∥AB

∴△NDP∽△BDA

∴=

∴NP=

②设⊙N与AD交于G，H，连接NG，则NG=NB=2，

在Rt△GNP中，由勾股定理可得：GP==

∴GH=2GP=

（3）当点M在⊙N的外部时，线段EM与⊙N只有1个公共点，则∠BEM≥90°，

若∠BEM=90°，则==，即5BE=3BM

∴5×2t=3（3﹣t），解得：t=

∴0＜t≤

当点M在⊙N的内部时，线段EM与⊙N也只有1个公共点，由①知，点F与点M重合时，t=，

∴＜t≤

故t的取值范围为：0＜t≤或＜t≤．