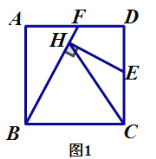
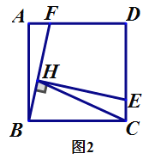
题目内容
【题目】在学习完概率的有关内容后,小军与小波共同发明了一种利用“字母棋”进行比胜负的游戏,他们制作了5颗棋子,并在每颗棋子上标注相应的字母(棋子除了字母外,材质、大小、质地均相同),其中标有字母X的棋子有1颗,标有字母Y和Z的棋子分别有2颗.游戏规定:将5颗棋子放入一个不透明的袋子中,然后从5颗棋子中随机摸出两颗棋子,若摸到的两颗棋子标有字母X,则小军胜;若摸到两颗相同字母的棋子,则小波胜,其余情况为平局,则游戏重新进行.
(1)求随机摸到标有字母Y的棋子的概率;
(2)在游戏刚准备进行的同时,数学课代表小亮对游戏的公平性产生了质疑,请你通过列表法或者画树状图的方法帮小亮同学验证该游戏的规则是否公平.
【答案】(1)![]() ;(2)游戏的规则不公平,理由详见解析
;(2)游戏的规则不公平,理由详见解析
【解析】
(1)利用概率公式计算可得;
(2)首先根据题意列出表格,然后由表格求得小军胜与小波胜的概率,比较概率的大小,即可得这个游戏是否公平;使游戏规则游戏公平,只要使得小军胜与小波胜的概率相等即可.
解:(1)已知一共有5颗棋子,其中标有字母Y的棋子有2颗,
故随机摸到标有字母Y的棋子的概率P=![]() .
.
(2)记标有字母Y的棋子分别为Y1,Y2,标有字母Z的棋子为Z1,Z2,
列表得
X | Y1 | Y2 | Z1 | Z2 | |
X | ﹣﹣ | (X,Y1) | (X,Y2) | (X,Z1) | (X,Z2) |
Y1 | (Y1,X) | ﹣﹣ | (Y1,Y2) | (Y1,Z1) | (Y1,Z2) |
Y2 | (Y2,X) | (Y2,Y1) | ﹣﹣ | (Y2,Z1) | (Y2,Z2) |
Z1 | (Z1,X) | (Z1,Y1) | (Z1,Y2) | ﹣﹣ | (Z1,Z2) |
Z2 | (Z2,X) | (Z2,Y1) | (Z2,Y2) | (Z2,Z1) | ﹣﹣ |
总共有20种等可能的情况.
其中摸到标有字母X的棋子的情况有8种,摸到标有两个相同字母的棋子的情况有4种,
故小军获胜的概率P1=![]() =
=![]() ,小波获胜的概率P2=
,小波获胜的概率P2=![]() =
=![]() ,
,
∵P1>P2,
∴该游戏的规则不公平.

 名校课堂系列答案
名校课堂系列答案【题目】某数学兴趣小组在探究函数y=|x2-4x+3|的图象和性质时,经历以下几个学习过程:
(1)列表(完成以下表格)
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y1=x2-4x+3 | … | 15 | 8 | 0 | 0 | 3 | 15 | … | |||
y=|x2-4x+3| | … | 15 | 8 | 0 | 0 | 3 | 15 | … |
(2)描点并画出函数图象草图(在备用图1中描点并画图)

(3)根据图象完成以下问题
(ⅰ)观察图象
函数y=|x2-4x+3|的图象可由函数y1=x2-4x+3的图象如何变化得到?
答:______.
(ⅱ)数学小组探究发现直线y=8与函数y=|x2-4x+3|的图象交于点E、F,E(-1,8),F(5,8),则不等式|x2-4x+3|>8的解集是______;
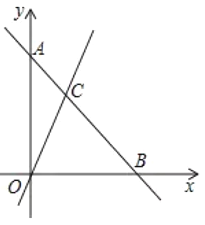
(ⅲ)设函数y=|x2-4x+3|的图象与x轴交于A、B两点(B位于A的右侧),与y轴交于点C.
①求直线BC的解析式;
②探究应用:将直线BC沿y轴平移m个单位后与函数y=|x2-4x+3|的图象恰好有3个交点,求此时m的值.
【题目】某校为了预测本校九年级男生毕业体育测试达标情况,随机抽取该年级部分男生进行了一次测试(满分50分,成绩均记为整数分),并按测试成绩![]() (单位:分)分成四类:
(单位:分)分成四类:![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
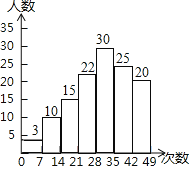
类(![]() )绘制出如图所示的不完整条形统计图,请根据图中信息解答下列问题:
)绘制出如图所示的不完整条形统计图,请根据图中信息解答下列问题:
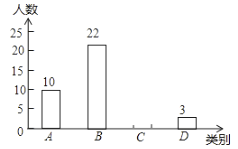
成绩等级 | 人数 | 所占百分比 |
| 10 |
|
| 22 |
|
|
|
|
| 3 |
|
(1)![]() ______,
______,![]() _______,
_______,![]() _________;
_________;
(2)补全条形统计图;
(3)若该校九年级男生有600名,![]() 类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?
类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?