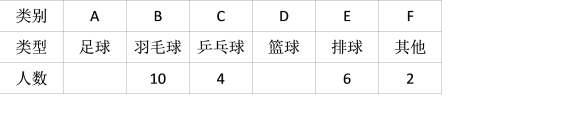题目内容
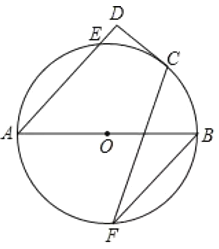
【题目】如图，在
中，
点
是
边上一点，连接
，以
为直径的
交于点
则线段
的最小值为（ ）
A.
B.
C.
D.
【答案】D
【解析】
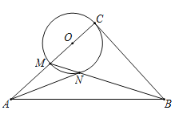
连接CN，根据直径所对的圆周角是直角可得∠CNM=90°，然后根据圆周角为直角所对的弦为直径可得点N的运动轨迹为以BC为直径的圆上的一部分，设圆心为O′，连接AO′，交圆O′于点N，易知此时AN最小，然后利用勾股定理求出AO′即可求出结论．
解：连接CN
∵CM为直径
∴∠CNM=90°
∴∠CNB=180°－∠CNM=90°
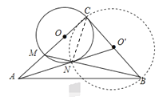
∴点N的运动轨迹为以BC为直径的圆上的一部分，设圆心为O′，如下图所示，连接AO′，交圆O′于点N，易知此时AN最小
∵
∴O′C= O′N=
1
根据勾股定理可得：AO′=
∴此时AN=AO′－O′N=
即线段
的最小值为
故选D．
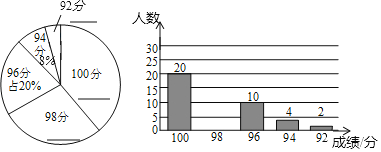
阅读快车系列答案
【题目】为提升学生的艺术素养，某校计划开设四门选修课程：声乐、舞蹈、书法、摄影．要求每名学生必须选修且只能选修一门课程，为保证计划的有效实施，学校随机对部分学生进行了一次调查，并将调査结果绘制成如下不完整的统计表和统计图．
学生选修课程统计表
课程 | 人数 | 所占百分比 |
声乐 | 14 |
|
舞蹈 | 8 |
|
书法 | 16 |
|
摄影 |
|
|
合计 |
|
|
根据以上信息，解答下列问题：
（1）
，
．
（2）求出
的值并补全条形统计图．
（3）该校有1500名学生，请你估计选修“声乐”课程的学生有多少名．
（4）七（1）班和七（2）班各有2人选修“舞蹈”课程且有舞蹈基础，学校准备从这4人中随机抽取2人编排“舞蹈”在开班仪式上表演，请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率．
【题目】某厂按用户的月需求量
（件）完成一种产品的生产，其中
.每件的售价为18万元，每件的成本
（万元）是基础价与浮动价的和，其中基础价保持不变，浮动价与月需求量（件）成反比.经市场调研发现，月需求量与月份
（为整数，
）符合关系式
（
为常数），且得到了表中的数据.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
（1）求与满足的关系式，请说明一件产品的利润能否是12万元；
（2）求，并推断是否存在某个月既无盈利也不亏损；
（3）在这一年12个月中，若第
个月和第
个月的利润相差最大，求
.
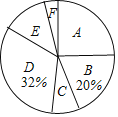
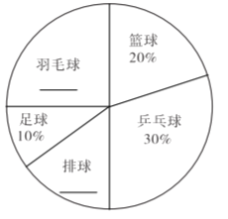
【题目】某校设有体育选修课，每位同学必须从羽毛球、篮球、乒乓球、排球、足球五项球类运动中 选择一项且只能选择一项球类运动，在该校学生中随机抽取10% 的学生进行调查，根据调查 结果绘制成如图所示的尚不完整的频数分布表和扇形统计图．
运动项目 | 频数 |
羽毛球 |
|
篮球 |
|
兵乓球 |
|
排球 |
|
足球 |
|
请根据以上图、表信息解答下列问题:
（1）频数分布表中的
，
；
（2）补全扇形统计图；
（3）排球所在的扇形的圆心角为 度；
（4）全校有多少名学生选择参加乒乓球运动?