Question

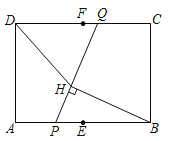
【题目】如图，在矩形中，，，，分别为，边的中点．动点从点出发沿向点运动，同时，动点从点出发沿向点运动，连接，过点作于点，连接．若点的速度是点的速度的2倍，在点从点运动至点的过程中，线段长度的最大值为_________，线段长度的最小值为_________．

Answer 1

【答案】

【解析】

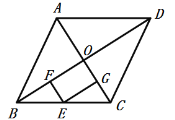
连接EF，则EF⊥AB，过点P作PG⊥CD于点G，如图1，由于，而PG=3，所以当GQ最大时PQ最大，由题意可得当P、A重合时GQ最大，据此即可求出PQ的最大值；设EF与PQ交于点M，连接BM，取BM的中点O，连接HO，如图2，易证△FQM∽△EPM，则根据相似三角形的性质可得EM为定值2，于是BM的长度可得，由∠BHM=∠BEM=90°可得B、E、H、M四点共圆，且圆心为点O，于是当D、H、O三点共线时，DH的长度最小，最小值为DO－OH，为此只需连接DO，求出DO的长即可，可过点O作ON⊥CD于点N，作OK⊥BC于点K，如图3，构建Rt△DON，利用勾股定理即可求出DO的长，进而可得答案．

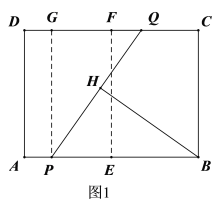
解：连接EF，则EF⊥AB，过点P作PG⊥CD于点G，如图1，则PE=GF，PG=AD=3，

设FQ=t，则GF=PE=2t，GQ=3t，

在Rt△PGQ中，由勾股定理得：，

∴当t最大即EP最大时，PQ最大，

由题意知：当点P、A重合时，EP最大，此时EP=2，则t=1，

∴PQ的最大值=；

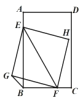
设EF与PQ交于点M，连接BM，取BM的中点O，连接HO，如图2，

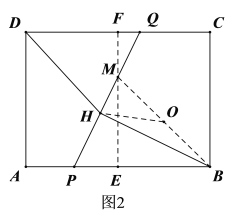
∵FQ∥PE，∴△FQM∽△EPM，

∴，

∵EF=3，

∴FM=1，ME=2，

∴，

∵∠BHM=∠BEM=90°，

∴B、E、H、M四点共圆，且圆心为点O，

∴，

∴当D、H、O三点共线时，DH的长度最小，

连接DO，过点O作ON⊥CD于点N，作OK⊥BC于点K，如图3，则OK=BK=1，

∴NO=2，CN=1，∴DN=3，

则在Rt△DON中，，

∴DH的最小值=DO－OH=．

故答案为：，．