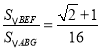题目内容
【题目】在平面直角坐标系xOy中，A（t，0），B（t+4，0），线段AB的中点为C，若平面内存在一点P使得∠APC或者∠BPC为直角（点P不与A，B，C重合），则称P为线段AB的直角点．
（1）当t=0时，
①在点P1（
，0），P2（，
），P3（
，﹣）中，线段AB的直角点是 ；
②直线y=
x+b上存在四个线段AB的直角点，直接写出b取值范围；
（2）直线y=x+1与x，y轴交于点M，N．若线段MN上只存在两个线段AB的直角点，直接写出t取值范围．
【答案】（1）①
，
②
或
（2）
或
【解析】
（1）由线段AB的直角点定义可求解；
（2）由圆周角定理可得点P在以BC为直径或AC为直径的圆上，求出直线y=
x+b过点C时，b的值和直线y=x+b与以BC为直径或AC为直径的圆相切时，b的值，即可求解．
（3）由题意可得以BC为直径或AC为直径的圆与线段MN的交点只有两个，利用特殊位置可求解．
解：（1）①当t=0时，则点A（0，0），点B（4，0），
∵点C是AB中点，
∴点C（2，0），
∴AC=BC=2，
∵AP12+CP12=
+
≠AC2=4，
∴点P1不是线段AB的直角点；
∵AP22+CP22=+
++=4=AC2=4，
∴∠AP2B=90°，
∴点P2是线段AB的直角点，
∵CP32+BP32=+++=4=BC2=4，
∴∠CP3B=90°，
∴点P3是线段AB的直角点，
故答案为：P2，P3；
②∵∠APC或者∠BPC为直角，
p>∴点P在以BC为直径或AC为直径的圆上，如图，当直线y=x+b与以AC为直径的圆相切时，直线y=x+b与以AC为直径的圆和以BC为直径的圆有三个交点，即存在三个线段AB的直角点，
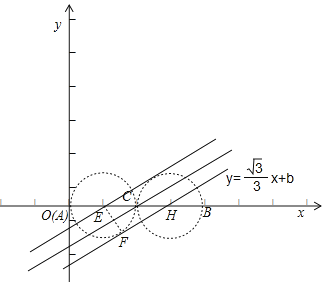
设切点为F，以AC为直径的圆的圆心为E，直线y=x+b与x轴交于点H，连接EF，
∵直线y=x+b与以AC为直径的圆相切，
∴EF⊥FH，
∵直线y=x+b与x轴所成锐角为30°，
∴EH=2EF=2，
∴点H（3，0），
∴0=×3+b，
∴b=﹣
，
同理可得，当直线y=x+b与以BC为直径的圆相切时，b=﹣，
当直线y=x+b过点C时，直线y=x+b与以AC为直径的圆和以BC为直径的圆有三个交点，即直线y=x+b上存在三个线段AB的直角点，
∴0=
+b，
∴b=﹣，
∴当﹣＜b＜﹣或﹣＜b＜﹣时，直线y=x+b与以AC为直径的圆和以BC为直径的圆有四个交点，即直线y=x+b上存在四个线段AB的直角点，
（2）∵直线y=x+1与x，y轴交于点M，N，
∴点N（0，1），点M（﹣，0），
如图，当直线y=x+1与以BC为直径的圆相切于点F，设BC为直径的圆的圆心为E，连接EF，此时线段MN与以AC为直径的圆和以BC为直径的圆有两个交点，即线段MN上存在两个线段AB的直角点，
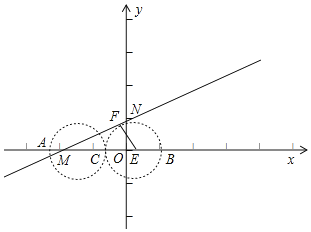
∵A（t，0），B（t+4，0），点C是线段AB的中点，
∴AB=4，AC=BC=2，
∵直线y=x+1与以BC为直径的圆相切于点F，
∴EF⊥MN，
∵∠NMB=30°，
∴ME=2EF=2，
∴点E（﹣+2，0），
∴点A（﹣﹣1，0），
∴t=﹣﹣1
当直线y=x+1与以AC为直径的圆相切时，此时线段MN与以AC为直径的圆和以BC为直径的圆有3个交点，即线段MN上存在3个线段AB的直角点，
同理可求：t=1﹣，
当点A与点M重合时，此时线段MN与以AC为直径的圆和以BC为直径的圆有两个交点，即线段MN上存在两个线段AB的直角点，
∴当﹣＜t＜1﹣或t=﹣﹣1时，线段MN上只存在两个线段AB的直角点．
【点晴】
本题考查了一次函数的综合应用，角的计算，圆周角定理以及切线的性质；解题的关键是懂得点P在以BC为直径或AC为直径的圆上，以此来解决此题，此题综合性较强，与切线的性质练习较大，在日常练习中应加强训练．
