Question

【题目】画图（要求：以下操作均只使用无刻度的直尺）

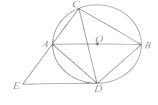
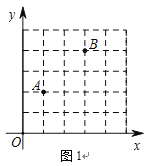
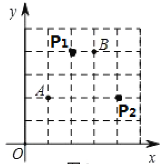
（1）在直角坐标系中我们把横、纵坐标都为整数的点称为整点．如图1中点A（1，2）、B（3，4），在图1中第一象限内找出所有的整点P（图上标为P1、P2），使得点P横、纵坐标的平方和等于20．

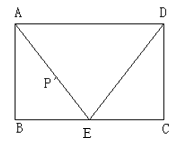
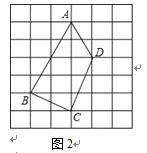
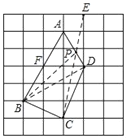
（2）如图2，是大小相等的边长为1的正方形构成的网格，A、B、C、D均为格点．请在线段AD上找一点P，并连结BP使得直线BP将四边形ABCD的面积分为1：2两部分，在图中画出线段BP，并简要说明你的画图方法．

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）设P（x,y），由题意得x2+y2=20,求出整数即可解决问题；（2）连接BD，先求出△ABD的面积与四边形ABCD的面积，由BQ使得直线BQ将四边形ABCD的面积分为1：2两部分得出△ABP的面积为，得出即S△ABD=S△ABD，也是AP：PD=5：3，所以连接CE，交AD于点P，连接BP，BP为 所求.

解：（1）设P（x,y），由题意得x2+y2=20,

∴x=4,y=2,或者x=2,y=4.

在直角坐标系表示为：

（2）如图，连接BD，则△ABD的面积=△ADF的面积+△BDF的面积=4，

四边形ABCD的面积=△ACD的面积+△ACB的面积=+×5×2=，

∵直线BP将四边形ABCD的面积分为1：2两部分，

∴△ABP的面积=×=，即S△ABD=S△ABD，∴AP：PD=5：3，

如图，连接CE，交AD于点P，连接BP，则，

∴线段BP即为所求．