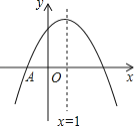题目内容
【题目】中国古贤常说万物皆自然,而古希腊学者说万物皆数.同学们还记得我们最初接触的数就是“自然数”吧!在数的学习过程中,我们会对其中一些具有某种特性的自然数进行研究,我们研究了奇数、偶数、质数、合数等.现在我们来研究另一种特珠的自然数—“![]() 喜数”.
喜数”.
定义:对于一个两位自然数,如果它的个位和十位上的数字均不为零,且它正好等于其个位和十位上的数字的和的![]() 倍(
倍(![]() 为正整数),我们就说这个自然数是一个“
为正整数),我们就说这个自然数是一个“![]() 喜数”.
喜数”.
例如:24就是一个“4喜数”,因为![]()
25就不是一个“![]() 喜数”因为
喜数”因为![]()
(1)判断44和72是否是“![]() 喜数”?请说明理由;
喜数”?请说明理由;
(2)试讨论是否存在“7喜数”若存在请写出来,若不存在请说明理由.
【答案】(1)44不是一个“![]() 喜数”, 72是一个“8喜数”,理由见解析;(2)“7喜数”有4个:21、42、63、84
喜数”, 72是一个“8喜数”,理由见解析;(2)“7喜数”有4个:21、42、63、84
【解析】
(1)根据“n喜数”的定义解答即可;
(2)设存在“7喜数”,设其个位数字为a,十位数字为b,(a,b为1到9的自然数),则10b+a=7(a+b),化简得:b=2a,由此即可得出结论.
(1)44不是一个“![]() 喜数”,因为
喜数”,因为![]() ,
,
72是一个“8喜数”,因为![]() ;
;
(2)设存在“7喜数”,设其个位数字为![]() ,
,
十位数字为![]() ,(
,(![]() ,
,![]() 为1到9的自然数),
为1到9的自然数),
由定义可知:![]()
化简得:![]() 因为
因为![]() ,
,![]() 为1到9的自然数,
为1到9的自然数,
∴![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ;
;
∴“7喜数”有4个:21、42、63、84.

【题目】已知函数![]() ,请根据已学知识探究该函数的图象和性质过程如下:
,请根据已学知识探究该函数的图象和性质过程如下:
(1)该函数自变量的取值范围为;
(2)下表列出y与x的几组对应值,请在平面直角坐标系中描出下列各点,并画出函数图象;
x | … |
|
| -1 |
| 2 |
|
| … |
y | … | 3 | 2 | 1 |
|
|
|
| … |

(3)结合所画函数图象,解决下列问题:
①写出该函数图象的一条性质:;
②横、纵坐标均为整数的点称为整点,若直线y= -x+b的图象与该图象相交形成的封闭图形(包含边界)内刚好有6个整点,则b的取值范围为.