题目内容
【题目】如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB′= . 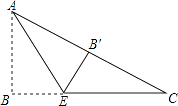
【答案】1.5
【解析】解:根据折叠可得BE=EB′,AB′=AB=3, 设BE=EB′=x,则EC=4﹣x,
∵∠B=90°,AB=3,BC=4,
∴在Rt△ABC中,由勾股定理得, ![]() ,
,
∴B′C=5﹣3=2,
在Rt△B′EC中,由勾股定理得,x2+22=(4﹣x)2 ,
解得x=1.5,
所以答案是:1.5.
【考点精析】掌握翻折变换(折叠问题)是解答本题的根本,需要知道折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
【题目】某学校开展“文明礼仪”演讲比赛,八(1)班、八(2)班派出的5名选手的比赛成绩如图所示.
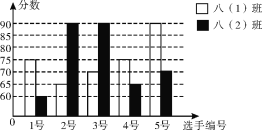
(1)根据上图,完成表格.
平均数 | 中位数 | 方差 | |
八(1)班 | 75 | _______ | _______ |
八(2)班 | 75 | 70 | 160 |
(2)结合两班选手成绩的平均数和方差,分析两个班级参加比赛的选手的成绩.
(3)如果在每班参加比赛的选手中分别选出3人参加决赛,从平均分看,你认为哪个班的实力更强一些?并说明理由.