题目内容
【题目】（1）问题背景：已知，如图1，等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，AB=a，△ABC的面积为S，则有BC=
a，S=
a2．
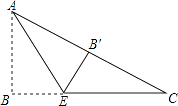
（2）迁移应用：如图2，△ABC和△ADE都是等腰三角形，∠BAC=∠DAE=120°，D，E，C三点在同一条直线上，连接BD．
①求证：△ADB≌△AEC；
②求∠ADB的度数．
③若AD=2，BD=4，求△ABC的面积．
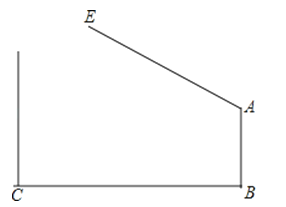
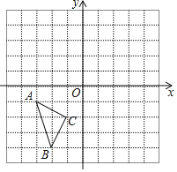
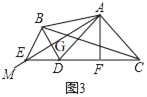
（3）拓展延伸：如图3，在等腰△ABC中，∠BAC=120°，在∠BAC内作射线AM，点D与点B关于射线AM轴对称，连接CD并延长交AM于点E，AF⊥CD于F，连接AD，BE．
①求∠EAF的度数；
②若CD=5，BD=2，求BC的长．
【答案】（1）详见解析；（2）①详见解析；②∠ADB=150°；③5
+6．；（3）①∠EAF=60°；②BC=
．
【解析】
（1）先判断出∠B=30°，BD=
BC，再利用三角函数得出BD=
AB，即可得出结论；
（2）①先判断出∠DAB=∠EAC，即可得出结论；
②先判断出∠ADB=∠AEC，再求出∠AEC，即可得出结论；
③先利用勾股定理求出EH，AH，再利用勾股定理求出AC2，借助（1）的结论即可得出结论；
（3）①先判断出∠BAE=∠DAE=∠BAD，∠DAF=∠CAF=∠CAD，即可得出∠EAF=∠BAC=60°，
②先求出DF=CD=2.5，再判断出△BDE是等边三角形，在Rt△AEF中，求出AE=3，在Rt△DEG中，EF=，∴AG=AE﹣EG=2，在Rt△ABG中，AB=
，即可得出结论．
解：（1）过点A作AD⊥BC于D，
∵AB=AC，∠BAC=120°，
∴BD=
BC，∠BAD=60°，
∴∠B=30°，cosB=
，
∴
=，
∴BD=AB，
∴BC=
AB=a．
∴S△ABC=
BC×AD=
a2；
（2）
①∵△ABC和△ADE都是等腰三角形，∠BAC=∠DAE=120°，
∴AD=AE，AB=AC，∠DAB=∠EAC，
在△ADB和△AEC中，
，
∴△ADB≌△AEC（SAS），
②由①知，△ADB≌△AEC，
∴∠ADB=∠AEC，
在△ADE中，∠DAE=120°，
∴∠AED=30°，
∴∠AEC=150°，
∴∠ADB=150°，
③如图2，过点A作AH⊥CD于H，
∴DH=EH，
在Rt△ADH中，∠ADE=30°，AD=2，
∴AH=1，
∴DH=EH=
，
由①知，△ADB≌△AEC，
∴CE=BD=4，
∴CH=CE+EH=4+，
在Rt△ACH中，AC2=AH2+CH2=20+8，
由（1）得，S△ABC=
AC2=×（20+8）=5
+6．
（3）①∵点B与点D关于AM对称，
∴∠BAE=∠DAE=
∠BAD，AB=AD，
∵AB=AC，
∴AD=AC，
∵AF⊥CE，
∴∠DAF=∠CAF=∠CAD，
∴∠EAF=∠DAE+∠DAF=∠BAD+∠CAD=（∠BAD+∠CAD）=∠BAC=60°，
②∵CD=5，
∴DF=CD=2.5，
由①知，∠AEF=90°﹣∠EAF=30°，
由对称得，BG=DG=BD=1，∠BED=2∠AEF=60°，BE=DE，
∴△BDE是等边三角形，
∴DE=BD=2，
∴EF=4.5，
在Rt△AEF中，cos∠AEF=
，
∴cos30°=
，
∴AE=3
，
在Rt△DEG中，EF=，
∴AG=AE﹣EG=2，
在Rt△ABG中，AB=
=
，
由（1）知，BC=AB=
．
