题目内容
【题目】按要求完成下列证明:
已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.
求证:DE∥BC.
证明:∵CD⊥AB(已知),
∴∠1+ =90°( ).
∵∠1+∠2=90°(已知),
∴ =∠2( ).
∴DE∥BC( ).
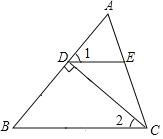
【答案】∠EDC;垂直定义;∠EDC;同角的余角相等;内错角相等,两直线平行.
【解析】
直接利用平行线的判定方法结合垂直的定义分析得出答案.
证明:∵CD⊥AB(已知),
∴∠1+∠EDC=90°( 垂直定义).
∵∠1+∠2=90°(已知),
∴∠EDC=∠2( 同角的余角相等).
∴DE∥BC( 内错角相等,两直线平行).
故答案为:∠EDC;垂直定义;∠EDC;同角的余角相等;内错角相等,两直线平行.

练习册系列答案
相关题目