题目内容
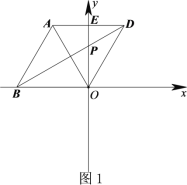
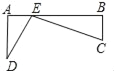
【题目】如图，铁路上A、B两点相距25km，C、D为两村庄，DA⊥AB于A，CB⊥AB于B，已知DA＝15km，CB＝10km，现在要在铁路AB上建一个土特产品收购站E，使得C、D两村到E站的距离相等，则E站应建在距A站多少千米处？
【答案】∵DA⊥AB
∴∠AED+∠D=900
∵DE⊥CE
∴∠AED+∠BEC=900
∴∠D=∠BEC
在
ADE和BEC中
∴
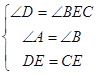
∴AE=BC=10 ∴E站应建在距A站10千米处。
【解析】
试题
设AE=
km，则BE=
km，在Rt△AED和Rt△BEC中，分别用勾股定理表达出：DE和CE，由DE=CE就可建立方程求解.
试题解析：
设AE=km，则由题意可得：BE=km，
∵DA⊥AB于点A，CB⊥AB于点B，
∴∠DAE=∠EBC=90°，
∴DE2=AE2+AD2=
+225，CE2=BE2+BC2=
+100，
又∵DE=CE，
∴
，解得：
.
即E站应建在距A站10km处.
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
