题目内容
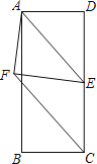
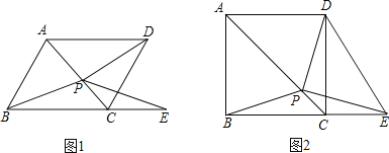
【题目】 如图1,P是菱形ABCD对角线AC上的一点,点E在BC的延长线上,且PE=PB.
(1)求证:PD=PE;
(2)求证:∠DPE=∠ABC;
(3)如图2,当四边形ABCD为正方形时,连接DE,试探究线段DE与线段BP的数量关系,并说明理由.
【答案】(1)详见解析;(2)详见解析;(3)DE=![]() BP,理由详见解析
BP,理由详见解析
【解析】
(1)根据菱形的性质得出BC=DC,∠BCP=∠DCP,然后利用“边角边”证明△BCP≌△DCP得出PB=PD,由已知PE=PB,即可得出结论;
(2)根据全等三角形对应角相等可得∠CBP=∠CDP,根据等边对等角可得∠CBP=∠E,然后求出∠DPE=∠DCE,再根据两直线平行,同位角相等可得∠DCE=∠ABC,从而得证;
(3)证出△PDE是等腰直角三角形,由等腰直角三角形的性质得出DE=![]() PE,即可得出结论.
PE,即可得出结论.
(1)证明:∵四边形ABCD是菱形,
∴BC=DC,∠BCP=∠DCP,AB∥DC,
∵在△BCP和△DCP中,
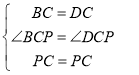 ,
,
∴△BCP≌△DCP(SAS),
∴PB=PD,
∵PE=PB,
∴PD=PE;
(2)证明:如图1所示:

由(1)知,△BCP≌△DCP,
∴∠CBP=∠CDP,
∵PE=PB,
∴∠CBP=∠E,
∵∠CFE=∠DFP(对顶角相等),
∴180°-∠DFP-∠CDP=180°-∠CFE-∠E,
即∠DPE=∠DCE,
∵AB∥CD,
∴∠DCE=∠ABC,
∴∠DPE=∠ABC;
(3)解:DE=![]() BP,理由如下:
BP,理由如下:
∵四边形ABCD是正方形,
∴∠ABC=90°,
由(1)知:PD=BP=PE,
由(2)知,∠DPE=∠ABC=90°,
∴△PDE是等腰直角三角形,
∴DE=![]() PE,
PE,
∴DE=![]() BP.
BP.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目